Explain Bagging Technique in Machine learning

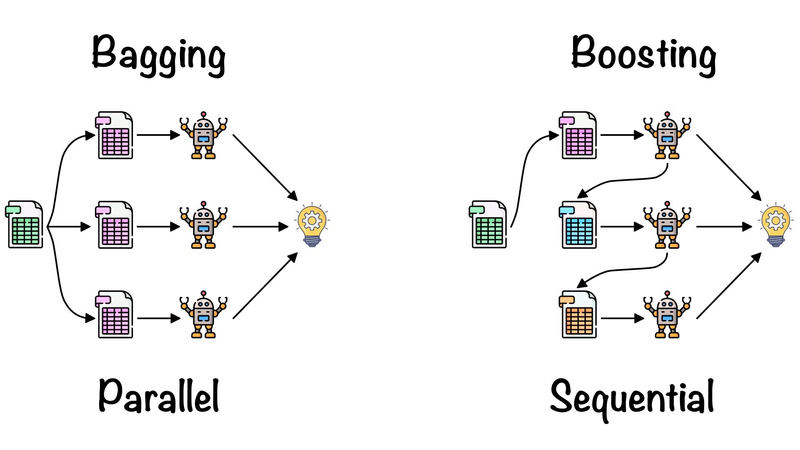
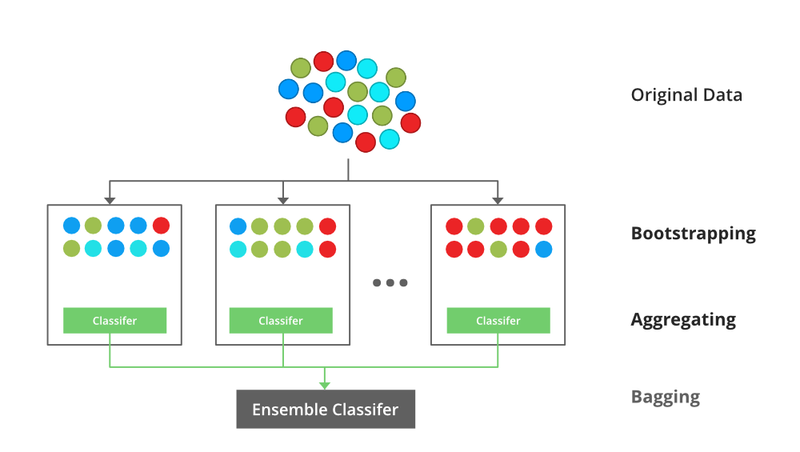
Bagging:
Bagging stands for Bootstrap Aggregating. In bagging, multiple learners are trained independently on different subsets of the training data, typically obtained by random sampling with replacement (bootstrap samples). The final prediction is made by aggregating the predictions of all individual models, such as taking a majority vote for classification tasks or averaging for regression tasks.

Example - Random Forest:

Random Forest is one of the most popular bagging ensemble methods. It combines multiple decision trees to create a more robust and accurate model. Each tree in the forest is trained on a different random subset of the training data and features. Let's see an example of Random Forest for a classification problem using scikit-learn:

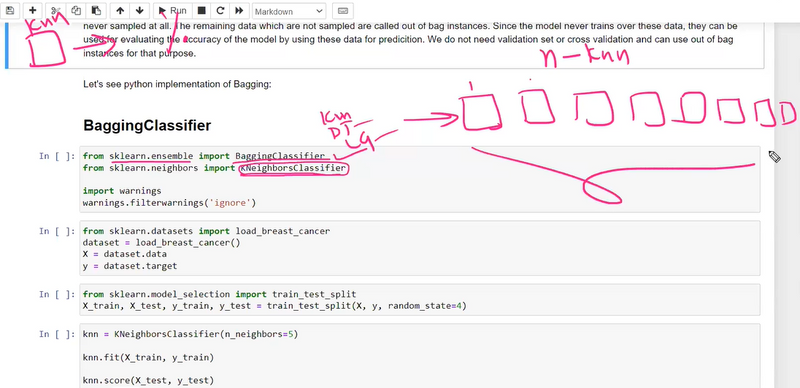
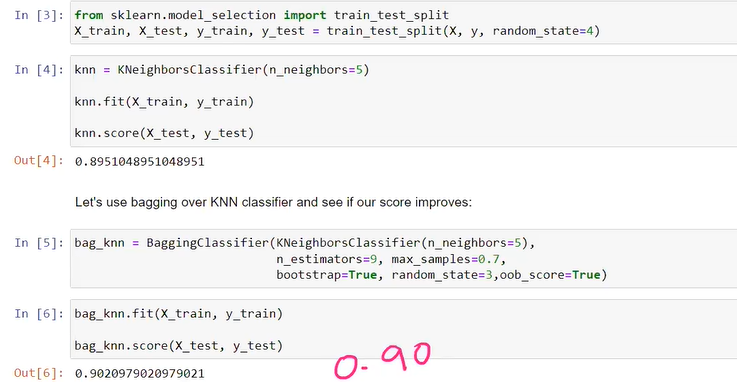
without pasting knn score

with pasting knn score

bagging classifier parameter explanation
he BaggingClassifier in scikit-learn is an ensemble learning method that combines multiple base classifiers (e.g., decision trees) into an ensemble. It uses bootstrap resampling (sampling with replacement) to create multiple subsets of the training data and trains a separate base classifier on each subset. The predictions from these base classifiers are then aggregated to make the final prediction. Here, I'll explain the parameters of the BaggingClassifier in detail with examples:

n_estimator == anything u can choose
neighbour
max_sample
random_state
bootstrap=true==pasting is false replacement allowed
if we have less or limited no of feature then we go bootstrap is false no need replacemenet pasting true

base_estimator:

The base estimator, which is the algorithm to use as the base learner. It can be any classifier.
Default: DecisionTreeClassifier()

base_classifier = DecisionTreeClassifier(max_depth=3)
bagging_classifier = BaggingClassifier(base_classifier)

n_estimators:

The number of base estimators (ensemble size).
Default: 10

bagging_classifier = BaggingClassifier(base_classifier, n_estimators=50)

max_samples:

The maximum number or proportion of samples to draw from the training dataset for each base estimator.
Default: 1.0 (use all samples)

bagging_classifier = BaggingClassifier(base_classifier, max_samples=0.7)

max_features:

The number or proportion of features to use for training each base estimator.
Default: 1.0 (use all features)

bagging_classifier = BaggingClassifier(base_classifier, max_features=0.5)

bootstrap:

Whether to use bootstrap sampling (with replacement) for creating subsets.
Default: True

bagging_classifier = BaggingClassifier(base_classifier, bootstrap=False)

bootstrap_features:

Whether to use bootstrap sampling for selecting features.
Default: False

bagging_classifier = BaggingClassifier(base_classifier, bootstrap_features=True)

oob_score:

Whether to calculate the out-of-bag (OOB) score for each base estimator. OOB score estimates the performance of the ensemble without the need for a separate validation set.
Default: False

bagging_classifier = BaggingClassifier(base_classifier, oob_score=True)

n_jobs:

The number of CPU cores to use for parallel execution during fitting and prediction. Set to -1 to use all available cores.

Default: 1
bagging_classifier = BaggingClassifier(base_classifier, n_jobs=-1)

random_state:

A random seed used for reproducibility.
Default: None

bagging_classifier = BaggingClassifier(base_classifier, random_state=42)

n_estimator

Determining the optimal value for the n_estimators hyperparameter in a Bagging Classifier (Bootstrap Aggregating) involves selecting the number of base learners (usually decision trees) to include in the ensemble. The goal is to find a balance between model complexity and predictive performance. Here's how you can determine the n_estimators parameter using cross-validation and an example:

Step 1: Import necessary libraries and load the dataset.

from sklearn.datasets import load_iris
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score

# Load a dataset (e.g., Iris dataset)
data = load_iris()
X = data.data
y = data.target

Step 2: Create a BaggingClassifier and evaluate its performance with different values of n_estimators.

# Define a range of values for n_estimators to test
n_estimators_values = [10, 50, 100, 200, 300]

# Create a list to store cross-validation scores for each value of n_estimators
cross_val_scores = []

# Loop through different n_estimators values
for n_estimators in n_estimators_values:
    # Create a BaggingClassifier with a base DecisionTreeClassifier
    bagging_classifier = BaggingClassifier(
        base_estimator=DecisionTreeClassifier(),  # Use a decision tree as the base model
        n_estimators=n_estimators,
        random_state=42
    )

    # Perform cross-validation and compute the mean accuracy
    scores = cross_val_score(bagging_classifier, X, y, cv=5)  # 5-fold cross-validation
    mean_accuracy = scores.mean()

    cross_val_scores.append(mean_accuracy)

Step 3: Visualize the results to find the optimal n_estimators.

import matplotlib.pyplot as plt

# Plot the cross-validated scores for different n_estimators values
plt.plot(n_estimators_values, cross_val_scores, marker='o')
plt.xlabel('n_estimators')
plt.ylabel('Mean Cross-Validated Accuracy')
plt.title('Performance vs. n_estimators')
plt.grid()
plt.show()

Step 4: Choose the optimal n_estimators value.

By examining the plot, you can identify the point at which the mean cross-validated accuracy stabilizes or reaches a peak. This point represents the optimal value for n_estimators. In the example, you would select the n_estimators value that corresponds to the highest mean accuracy.

Keep in mind that the optimal n_estimators value may vary depending on the dataset and problem. The goal is to find a value that balances model complexity and performance. You can also consider other performance metrics or use grid search or randomized search for a more automated hyperparameter tuning process.