In machine learning, model evaluation is a critical step to assess the performance and quality of a predictive model. There are various evaluation methods available, depending on the type of problem and the nature of the data. Here are some commonly used methods for model evaluation:
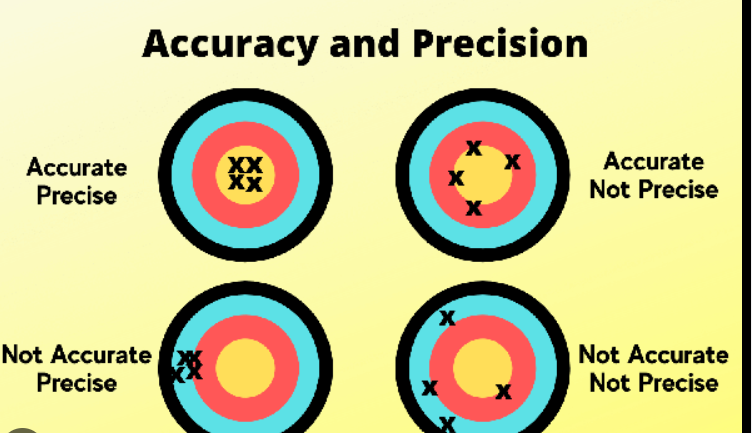
Accuracy: Accuracy is a widely used evaluation metric for classification problems. It measures the proportion of correct predictions made by the model out of the total predictions. However, accuracy alone may not be sufficient for imbalanced datasets where the classes are not equally represented.
Example: Let's say we have a binary classification problem to predict whether an email is spam or not. If a model correctly predicts 90 out of 100 spam emails and 800 out of 900 non-spam emails, the accuracy would be (90 + 800) / (100 + 900) = 89%.
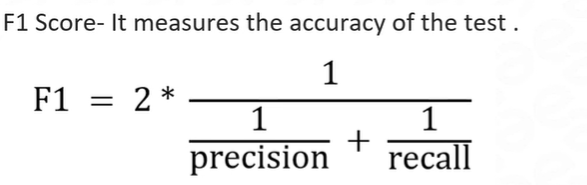
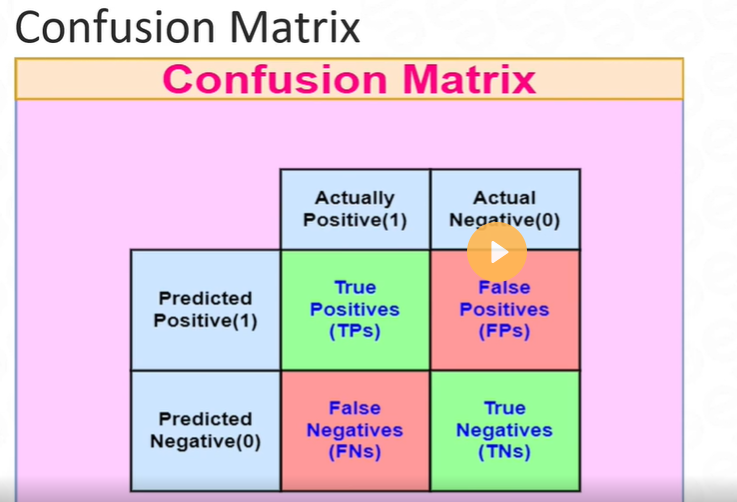
Precision, Recall, and F1-Score: Precision, recall, and the F1-score are evaluation metrics commonly used in binary classification problems, particularly when dealing with imbalanced datasets. These metrics provide insights into the model's performance with respect to true positives, false positives, and false negatives.
Precision: Precision measures the proportion of true positive predictions out of all positive predictions. It focuses on the correctness of positive predictions.
Recall: Recall, also known as sensitivity or true positive rate, measures the proportion of true positive predictions out of all actual positive instances. It focuses on the ability to correctly identify positive instances.
F1-score: The F1-score is the harmonic mean of precision and recall, providing a single metric that balances both precision and recall.
Example: In a medical diagnosis scenario, if a model predicts 100 positive cases, out of which 80 are actually positive (true positives), while 20 are false positives, the precision would be 80%. If there are a total of 150 actual positive cases, the recall would be 80/150 = 53.33%. The F1-score combines precision and recall, providing a single metric to evaluate the model's overall performance.
Mean Squared Error (MSE) and R-squared: These evaluation metrics are commonly used in regression problems.
Mean Squared Error (MSE): MSE measures the average squared difference between the predicted and actual values. It provides a measure of the model's accuracy in predicting continuous numerical values.
R-squared: R-squared, also known as the coefficient of determination, measures the proportion of the variance in the dependent variable that can be explained by the independent variables. It indicates how well the model fits the data.
Example: Suppose we have a regression model to predict housing prices. The MSE calculates the average squared difference between the predicted prices and the actual prices. R-squared measures the proportion of the variance in housing prices that can be explained by the model's features.
Cross-Validation: Cross-validation is a technique used to assess a model's performance on unseen data by partitioning the available data into multiple subsets or folds. It helps to estimate how well the model will generalize to new, unseen data.
Example: In k-fold cross-validation, the dataset is divided into k equally sized subsets. The model is trained on k-1 folds and evaluated on the remaining fold. This process is repeated k times, each time with a different fold used for evaluation. The performance metrics are then averaged across the k iterations to obtain an overall assessment of the model's performance.




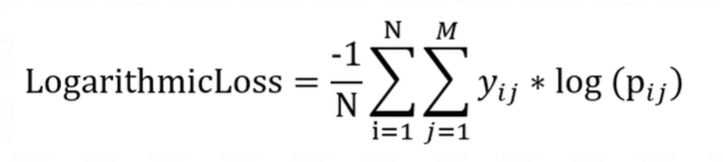

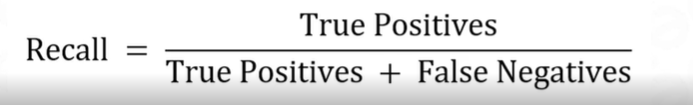




Top comments (0)