why we use stump
In the context of AdaBoost (Adaptive Boosting), the Gini index is not typically used to calculate the impurity of individual stumps (weak learners). Instead, the Gini index is commonly associated with decision trees, particularly when measuring impurity in decision tree nodes.
However, you can use alternative metrics like the misclassification rate or entropy to evaluate the performance of individual stumps in AdaBoost. The Gini index is typically used to evaluate the performance of the final AdaBoost ensemble.
Here's how you can calculate the misclassification rate for individual stumps in AdaBoost with an example:
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# Generate a synthetic dataset
X, y = make_classification(n_samples=100, n_features=2, random_state=42)
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create a base classifier (a decision tree with depth 1)
base_classifier = DecisionTreeClassifier(max_depth=1)
# Create an AdaBoost classifier
adaboost_classifier = AdaBoostClassifier(base_classifier, n_estimators=50, random_state=42)
# Train the AdaBoost classifier on the training data
adaboost_classifier.fit(X_train, y_train)
# Calculate the misclassification rate for individual stumps
individual_stump_errors = []
for stump in adaboost_classifier.estimators_:
stump_predictions = stump.predict(X_test)
stump_error = 1 - accuracy_score(y_test, stump_predictions)
individual_stump_errors.append(stump_error)
# Print the misclassification rates of individual stumps
for i, error in enumerate(individual_stump_errors):
print(f"Stump {i+1} Misclassification Rate: {error:.2f}")
In this example:
We generate a synthetic dataset and split it into training and testing sets.
We create a base classifier, which is a decision tree with a maximum depth of 1 (a decision stump).
We create an AdaBoost classifier using the base classifier and train it on the training data.
We calculate the misclassification rate for each individual stump in the AdaBoost ensemble by comparing their predictions to the true labels on the test data.
Finally, we print the misclassification rates of the individual stumps.
Keep in mind that in AdaBoost, the focus is on combining these individual stumps to create a strong ensemble learner. The Gini index is not typically used at the level of individual stumps but rather for evaluating the overall performance of the AdaBoost ensemble.
Why We use Stump
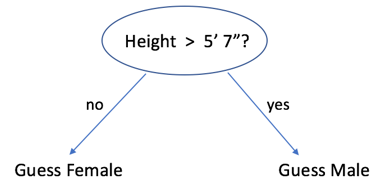
In machine learning, a "stump" refers to a simple and shallow decision tree with just one node and two leaf nodes (terminal nodes). A decision tree is a supervised machine learning algorithm used for both classification and regression tasks, where it partitions the data into subsets based on feature values and assigns a label or prediction to each subset.
A decision tree typically consists of a root node, internal nodes (decision nodes), and leaf nodes (terminal nodes). Each internal node represents a decision based on a feature, and each leaf node provides a final prediction or class label. In contrast, a stump is an extremely simplified version of a decision tree, and it has the following characteristics:
Single Decision Node: A stump has only one decision node (the root node), which means it evaluates a single feature and applies a threshold to make a decision.
Two Leaf Nodes: A stump has exactly two leaf nodes, one for each possible outcome of the decision made at the root node. These leaf nodes represent the final predictions or class labels.
Shallow Depth: Stumps have the shallowest possible depth for decision trees. They don't have any internal nodes beyond the root node.
Stumps are often used as weak learners in ensemble methods like AdaBoost and Gradient Boosting. Because stumps are very simple and have limited predictive power on their own, they are ideal candidates for boosting algorithms, which combine multiple weak learners (like stumps) to create a strong ensemble learner.
Here's a simple example of a decision stump:
Suppose you have a binary classification problem where you want to predict whether an email is spam (1) or not spam (0) based on a single feature: the number of times the word "free" appears in the email.
The root node of the stump may decide whether the word "free" appears more than or equal to 3 times in the email. If yes, it goes to one leaf node (predicting 1, which means spam); otherwise, it goes to the other leaf node (predicting 0, which means not spam).
So, a decision stump for this problem would look like:
If (number of times "free" >= 3):
Predict 1 (spam)
Else:
Predict 0 (not spam)
Stumps are used as building blocks in boosting algorithms because they can capture simple patterns in the data. Boosting then combines multiple stumps (or other weak learners) to create a strong and accurate predictive model.

Top comments (0)