Tensors are multi-dimensional data structures commonly used in mathematics, physics, and deep learning. In deep learning, tensors play a fundamental role in representing data and carrying out computations in neural networks. Here's a checklist of terminology related to tensors with examples:
Scalar (0D Tensor):
A single numerical value.
Example: 5
Vector (1D Tensor):
An ordered array of numbers.
Example: [1, 2, 3]
Matrix (2D Tensor):
A 2D array of numbers arranged in rows and columns.
Example:
lua
Copy code
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
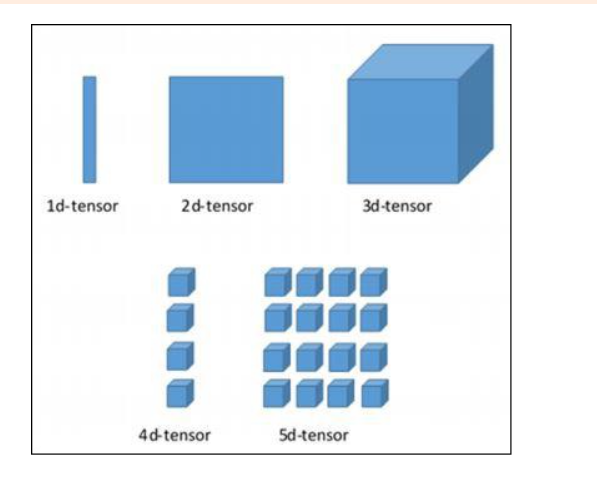
Tensor (N-Dimensional Tensor):
A generalization of matrices to more than two dimensions.
Example: A color image can be represented as a 3D tensor with dimensions (height, width, channels).
Shape:
The dimensions of a tensor, represented as a tuple or list.
Example: A matrix with shape (3, 4) has 3 rows and 4 columns.
Rank (or Order):
The number of dimensions in a tensor.
Example: A rank-2 tensor is a matrix, while a rank-3 tensor is a 3D array.
Element-wise Operation:
Operations performed on each element of a tensor separately.
Example: Element-wise addition of two matrices, where each corresponding element is added together.
Broadcasting:
Implicitly expanding the dimensions of tensors to make them compatible for element-wise operations.
Example: Adding a scalar to a matrix, where the scalar is broadcast to match the shape of the matrix.
Transpose:
Changing the dimensions of a tensor by switching its rows and columns.
Example: Transposing a matrix A changes the rows of A to columns and vice versa.
Reshape:
Changing the shape of a tensor while keeping the number of elements constant.
Example: Reshaping a 2x3 matrix into a 3x2 matrix.
Concatenation:
Combining tensors along a specified axis (dimension).
Example: Concatenating two 2D tensors along the rows or columns.
Tensor Product (or Outer Product):
A mathematical operation that combines two tensors to create a new tensor.
Example: The tensor product of two vectors results in a matrix.
Dot Product (Inner Product):
A specific type of element-wise multiplication and summation operation between tensors.
Example: The dot product of two vectors is a scalar value.
Reduction Operation:
Operations that reduce the dimensions of a tensor by aggregating values, e.g., sum, mean, max.
Example: Summing all elements of a tensor to get a scalar value.
Slicing:
Selecting specific elements or sub-tensors from a larger tensor.
Example: Extracting a portion of an image or a row from a matrix.
Sparse Tensor:
A tensor where most elements are zero or have negligible values.
Example: A document-term matrix in natural language processing where most entries are zeros.
Dense Tensor:
A tensor where most elements have non-zero values.
Example: A color image with RGB channels.
Gradient:
The derivative of a tensor with respect to some variable, used in training neural networks.
Example: Calculating the gradient of a loss function with respect to the model's parameters.
Placeholder:
A special type of tensor used to hold values that will be provided later, commonly used in TensorFlow and similar frameworks.
Example: A placeholder for input data in a deep learning model.

Top comments (0)