list out the checklist of Tensor RNN Operation in tensor flow

Explain the parameter of RNN

Basic RNN Layer - tf.keras.layers.SimpleRNN:

Example:

rnn_layer = tf.keras.layers.SimpleRNN(units=64, return_sequences=True)(input_data)

Output:
applying a basic RNN layer with 64 units and returning sequences for each time step.

Explanation

import tensorflow as tf

# Assume input_data is a 3-time step sequence with a feature dimension of 5
input_data = tf.constant([[[1.0, 2.0, 3.0, 4.0, 5.0],
                           [2.0, 3.0, 4.0, 5.0, 6.0],
                           [3.0, 4.0, 5.0, 6.0, 7.0]]], dtype=tf.float32)

# Create a Simple RNN layer
rnn_layer = tf.keras.layers.SimpleRNN(units=64, return_sequences=True)(input_data)

# Display the output shape of rnn_layer
print("Shape of rnn_layer:", rnn_layer.shape)

Shape of rnn_layer: (1, 3, 64)

This indicates that for each of the 3 time steps in the sequence, the RNN layer produces a vector of length 64. The return_sequences=True setting ensures that the full sequence of outputs is returned.
how we decide batch size and time step

The choice of batch size and the number of time steps depends on various factors, including the nature of your data, the requirements of your model, and the available computational resources. Let's discuss each aspect:

Batch Size:

1. The batch size is the number of samples (data points) used in each iteration of training.
2. Larger batch sizes often lead to faster training times, as computations can be parallelized more efficiently, but they may require more memory.
3. Smaller batch sizes can sometimes provide a regularization effect and may generalize better, but training can be slower.
4. Common batch sizes are powers of 2, such as 32, 64, 128, etc .

batch_size = 1  # Example batch size

Time Steps:

1. The number of time steps represents how many steps or observations are in a single sequence.
2. For sequential data, like time series or natural language sequences, choosing an appropriate number of time steps is crucial.
3. Too few time steps might result in the model not capturing long-term dependencies, while too many time steps can increase computational complexity and memory requirements .

num_time_steps = 3  # Example number of time steps

In the provided example, the input_data tensor has a shape of (1, 3, 5), where:

1 is the batch size (number of sequences in the batch).
3 is the number of time steps (length of each sequence).
5 is the feature dimension at each time step

.
So, for your specific use case, you need to consider the nature of your data. If your data is sequential (e.g., time series, text), you might choose a number of time steps that makes sense for capturing the temporal dependencies in your data.

Here's an example of adjusting the batch size and the number of time steps in the provided code:

import tensorflow as tf

# Example: Adjust batch size and number of time steps
batch_size = 2
num_time_steps = 4

# Create an example input_data tensor with the specified batch size and time steps
input_data = tf.constant(
    [[[1.0, 2.0, 3.0, 4.0, 5.0],
      [2.0, 3.0, 4.0, 5.0, 6.0],
      [3.0, 4.0, 5.0, 6.0, 7.0],
      [4.0, 5.0, 6.0, 7.0, 8.0]],
     [[9.0, 10.0, 11.0, 12.0, 13.0],
      [10.0, 11.0, 12.0, 13.0, 14.0],
      [11.0, 12.0, 13.0, 14.0, 15.0],
      [12.0, 13.0, 14.0, 15.0, 16.0]]], dtype=tf.float32)

# Create a Simple RNN layer with adjusted batch size and time steps
rnn_layer = tf.keras.layers.SimpleRNN(units=64, return_sequences=True)(input_data)

Feel free to adjust the batch_size and num_time_steps according to the characteristics of your data and the requirements of your model.

LSTM Layer - tf.keras.layers.LSTM:

Example:

lstm_layer = tf.keras.layers.LSTM(units=64, return_sequences=True)(input_data)

Output:
Applying an LSTM (Long Short-Term Memory) layer with 64 units and returning sequences.

Explanation

import tensorflow as tf

# Assume input_data is a 3-time step sequence with a feature dimension of 5
input_data = tf.constant([[[1.0, 2.0, 3.0, 4.0, 5.0],
                           [2.0, 3.0, 4.0, 5.0, 6.0],
                           [3.0, 4.0, 5.0, 6.0, 7.0]]], dtype=tf.float32)

# Create an LSTM layer
lstm_layer = tf.keras.layers.LSTM(units=64, return_sequences=True)(input_data)

# Display the output shape of lstm_layer
print("Shape of lstm_layer:", lstm_layer.shape)

after executing the code, the output shape of lstm_layer would be:

Shape of lstm_layer: (1, 3, 64)

This indicates that for each of the 3 time steps in the sequence, the LSTM layer produces a vector of length 64. The return_sequences=True setting ensures that the full sequence of outputs is returned.

GRU Layer - tf.keras.layers.GRU:

Example:

gru_layer = tf.keras.layers.GRU(units=64, return_sequences=True)(input_data)

Output:
Applying a GRU (Gated Recurrent Unit) layer with 64 units and returning sequences.

Explanation

import tensorflow as tf

# Assume input_data is a 3-time step sequence with a feature dimension of 5
input_data = tf.constant([[[1.0, 2.0, 3.0, 4.0, 5.0],
                           [2.0, 3.0, 4.0, 5.0, 6.0],
                           [3.0, 4.0, 5.0, 6.0, 7.0]]], dtype=tf.float32)

# Create a GRU layer
gru_layer = tf.keras.layers.GRU(units=64, return_sequences=True)(input_data)

# Display the output shape of gru_layer
print("Shape of gru_layer:", gru_layer.shape)

In this example:

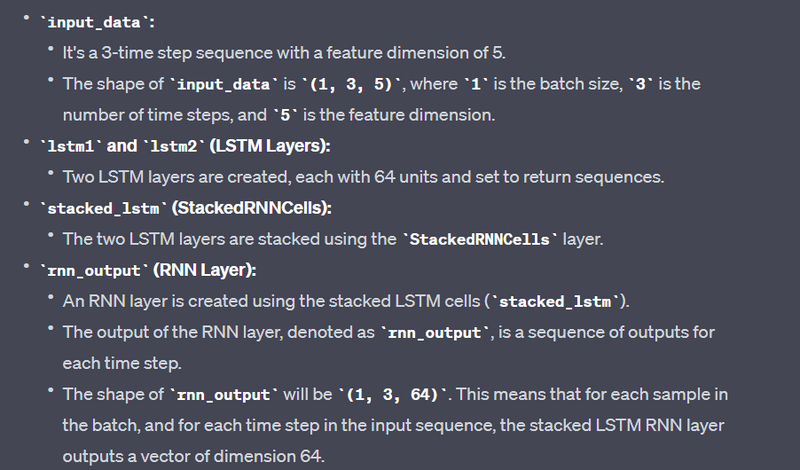
input_data:

It's a 3-time step sequence with a feature dimension of 5.
The shape of input_data is (1, 3, 5), where 1 is the batch size, 3 is the number of time steps, and 5 is the feature dimension.
gru_layer:

The GRU layer is applied to input_data with units=64 and return_sequences=True.

The output of the GRU layer, denoted as gru_layer, is a sequence of outputs for each time step.
The shape of gru_layer will be (1, 3, 64). This means that for each sample in the batch, and for each time step in the input sequence, the GRU layer outputs a vector of dimension 64.
So, after executing the code, the output shape of gru_layer would be:

Shape of gru_layer: (1, 3, 64)

Bidirectional RNN Layer - tf.keras.layers.Bidirectional:

Example:

bidirectional_rnn = tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64, return_sequences=True))(input_data)

Output:
Applying a bidirectional LSTM layer with 64 units and returning sequences.
Stacking RNN Layers - tf.keras.layers.StackedRNNCells:

Example:

lstm1 = tf.keras.layers.LSTM(64, return_sequences=True)
lstm2 = tf.keras.layers.LSTM(64, return_sequences=True)
stacked_lstm = tf.keras.layers.StackedRNNCells([lstm1, lstm2])
rnn_output = tf.keras.layers.RNN(stacked_lstm)(input_data)

Output:
Stacking multiple LSTM layers to create a deep RNN.

import tensorflow as tf

# Assume input_data is a 3-time step sequence with a feature dimension of 5
input_data = tf.constant([[[1.0, 2.0, 3.0, 4.0, 5.0],
                           [2.0, 3.0, 4.0, 5.0, 6.0],
                           [3.0, 4.0, 5.0, 6.0, 7.0]]], dtype=tf.float32)

# Create two LSTM layers
lstm1 = tf.keras.layers.LSTM(64, return_sequences=True)
lstm2 = tf.keras.layers.LSTM(64, return_sequences=True)

# Stack the LSTM layers
stacked_lstm = tf.keras.layers.StackedRNNCells([lstm1, lstm2])

# Create an RNN layer with the stacked LSTM cells
rnn_output = tf.keras.layers.RNN(stacked_lstm)(input_data)

# Display the output shape of rnn_output
print("Shape of rnn_output:", rnn_output.shape)

output

Shape of rnn_output: (1, 3, 64)

RNN Sequence Generation - Custom Implementation:

Example:

rnn = tf.keras.layers.SimpleRNN(64, return_sequences=True)
initial_state = rnn.get_initial_state(input_data)
sequence = [input_data]
for _ in range(sequence_length):
    output, new_state = rnn(sequence[-1], initial_state)
    sequence.append(output)

Output:
Generating an RNN sequence one step at a time.

Explanation

import tensorflow as tf

# Assume input_data is a 3-time step sequence with a feature dimension of 5
input_data = tf.constant([[[1.0, 2.0, 3.0, 4.0, 5.0],
                           [2.0, 3.0, 4.0, 5.0, 6.0],
                           [3.0, 4.0, 5.0, 6.0, 7.0]]], dtype=tf.float32)

# Create a SimpleRNN layer
rnn = tf.keras.layers.SimpleRNN(64, return_sequences=True)

# Get the initial state of the RNN
initial_state = rnn.get_initial_state(input_data)

# Initialize a sequence with the input data
sequence = [input_data]

# Define the length of the sequence
sequence_length = 5  # Example length

# Loop to generate the RNN sequence
for _ in range(sequence_length):
    output, new_state = rnn(sequence[-1], initial_state)
    sequence.append(output)

# Display the shape of the last element in the sequence
print("Shape of the last element in the sequence:", sequence[-1].shape)

Shape of the last element in the sequence: (1, 3, 64)

This indicates that for each of the 3 time steps in the sequence, the Simple RNN layer produces a vector of length 64.

Custom RNN Cell - tf.keras.layers.AbstractRNNCell:

Example:

class MyRNNCell(tf.keras.layers.AbstractRNNCell):
    def __init__(self, units):
        super(MyRNNCell, self).__init__()
        self.units = units

    def call(self, inputs, state):
        new_state = inputs + state
        output = new_state
        return output, new_state

rnn_layer = tf.keras.layers.RNN(MyRNNCell(64), return_sequences=True)(input_data)

Output: Creating a custom RNN cell and using it in an RNN layer.
These are some common RNN operations in TensorFlow, used for sequence modeling and time-series data analysis. The specific RNN architecture and configuration can vary depending on the application and problem domain.

Explain the parameter of RNN

Recurrent layers are crucial in handling sequential data in deep learning, where the order of the input data matters. Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks are common examples of architectures that use recurrent layers. Here are the main parameters/arguments of recurrent layers, along with examples:

Units (or units):

Definition: The dimensionality of the output space (i.e., the number of output units in the layer).
Example:

from tensorflow.keras.layers import SimpleRNN

model.add(SimpleRNN(units=64, input_shape=(10, 32)))

This creates a SimpleRNN layer with 64 units, and the input data is expected to have a shape of (batch_size, 10, 32).

Activation Function (or activation):

Definition: The activation function applied to the output of the recurrent layer.
Example:

model.add(SimpleRNN(units=128, activation='tanh', input_shape=(20, 64)))

This creates a SimpleRNN layer with 128 units and applies the hyperbolic tangent (tanh) activation function.

Use Bias (or use_bias):

Definition: A boolean indicating whether to include a bias term in the layer.
Example:

model.add(SimpleRNN(units=32, use_bias=True, input_shape=(8, 16)))

This creates a SimpleRNN layer with 32 units and includes a bias term.
Kernel Regularizer (or kernel_regularizer):

Definition: Regularizer function applied to the kernel weights matrix.
Example:

from tensorflow.keras.regularizers import l2

model.add(SimpleRNN(units=64, kernel_regularizer=l2(0.01), input_shape=(15, 128)))

This creates a SimpleRNN layer with 64 units and applies L2 regularization with a regularization strength of 0.01 to the kernel weights.

Recurrent Regularizer (or recurrent_regularizer):

Definition: Regularizer function applied to the recurrent weights matrix.
Example:

from tensorflow.keras.regularizers import l1

model.add(SimpleRNN(units=128, recurrent_regularizer=l1(0.001), input_shape=(25, 32)))

This creates a SimpleRNN layer with 128 units and applies L1 regularization with a regularization strength of 0.001 to the recurrent weights.
Bias Regularizer (or bias_regularizer):

Definition: Regularizer function applied to the bias vector.
Example:

from tensorflow.keras.regularizers import l1_l2

model.add(SimpleRNN(units=32, bias_regularizer=l1_l2(l1=0.001, l2=0.01), input_shape=(12, 64)))

This creates a SimpleRNN layer with 32 units and applies a combination of L1 and L2 regularization to the bias vector.
Return Sequences (or return_sequences):

Definition: A boolean indicating whether to return the full sequence (output at each time step) or just the last output.
Example:

model.add(SimpleRNN(units=64, return_sequences=True, input_shape=(30, 128)))

This creates a SimpleRNN layer with 64 units and returns the full sequence.
Return State (or return_state):

Definition: A boolean indicating whether to return the last state in addition to the output.
Example:

model.add(SimpleRNN(units=128, return_state=True, input_shape=(40, 64)))

This creates a SimpleRNN layer with 128 units and returns both the output sequence and the last state.
These parameters collectively define the behavior of recurrent layers in a neural network. Depending on the task and the characteristics of the sequential data, you can adjust these parameters to customize the architecture of your recurrent neural network.