Characteristics of an Algorithm

algorithm
characteristics-of-an-algorithm
big-o-notation-in-data-structure-article
big-o-notation
big-o-notation-in-data-structures

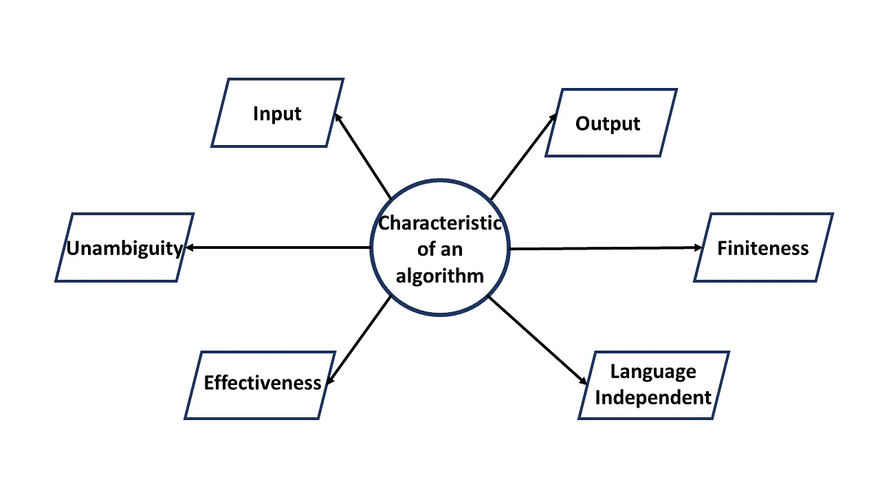
There are some characteristics which every algorithm should follow.There are five different characteristics which deal with various aspects of algorithm.They are as follows:

Input specified

Output specified

Definiteness

Effectiveness

Finiteness

Independent

Let us see these characteristics one by one.

Input specified
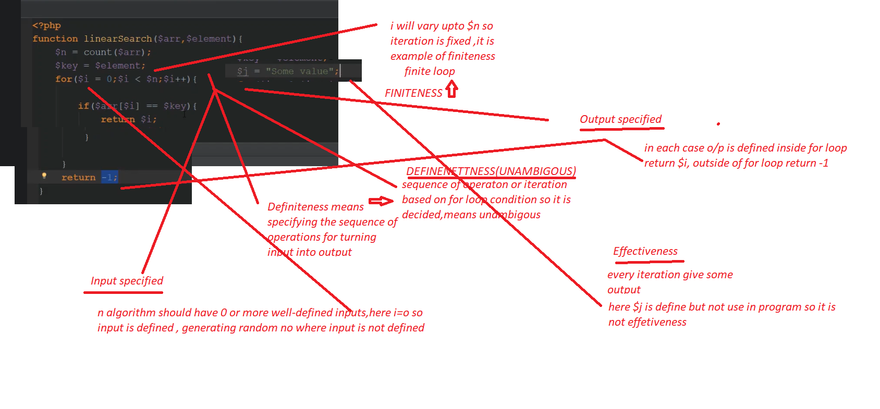
The input is the data to be transformed during the computation to produce the output.An algorithm should have 0 or more well-defined inputs.Input precision requires that you know what kind of data, how much and what form the data should be

Output specified
The output is the data resulting from the computation (your intended result). An algorithm should have 1 or more well-defined outputs, and should match the desired output.Output precision also requires that you know what kind of data, how much and what form the output should be (or even if there will be any output at all!).

Definiteness
Algorithms must specify every step and the order the steps must be taken in the process.Definiteness means specifying the sequence of operations for turning input into output. Algorithm should be clear and unambiguous.Details of each step must be also be spelled out (including how to handle errors).It should contain everything quantitative and not qualitative.

You could not expect a computer to understand something if you yourself are ambiguous about it.Right!

Effectiveness
For an algorithm to be effective, it means that all those steps that are required to get to output must be feasible with the available resources.It should not contain any unnecessary and redundant steps which could make an algorithm ineffective.

For example,suppose you are cooking a recipe and you chop vegetables which are not be used in the recipe then it is a waste of time.

Finiteness
The algorithm must stop, eventually.Stopping may mean that you get the expected output OR you get a response that no solution is possible. Algorithms must terminate after a finite number of steps.An algorithm should not be infinite and always terminate after definite number of steps.

There is no point in developing an algorithm which is infinite as it will be useless for us.

Independent
An algorithm should have step-by-step directions, which should be independent of any programming code.It should be such that it could be run on any of the programming languages.

Understanding Big O notation

Big O notation is an asymptotic analysis that describes how long an algorithm takes to perform. In other words, it’s used to talk about how efficient or complex an algorithm is.

Big O describes the execution time, or run time, of an algorithm relative to its input N
N
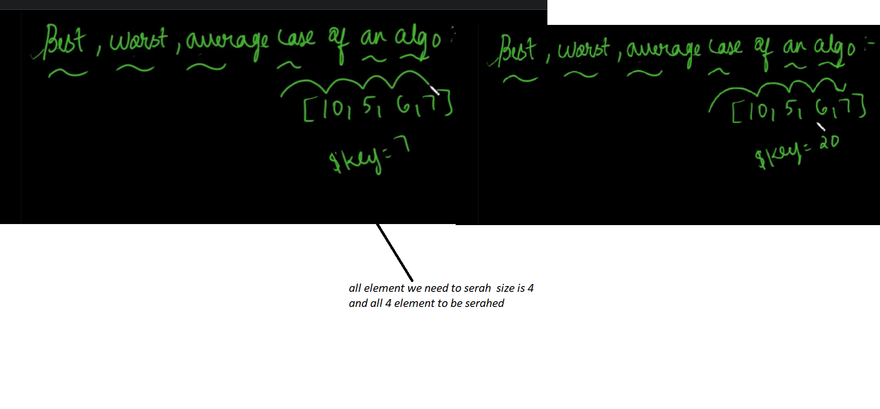
as the input increases. Though we can analyze an algorithm’s efficiency using average-case and best-case, we typically use worst-case with Big O notation.

Today, you will learn about time complexity, but take note that space complexity is also an important concept to understand. Runtime complexity can be a difficult concept to grasp at first, so let’s look at some examples.

O(1)

public int findInt(int[] arr) {
    return arr[0];
}

O(1) describes an algorithm that always runs at a constant time no matter its input. The function will execute at the same time no matter if the array holds a thousand integers or one integer because it only takes one “step”.

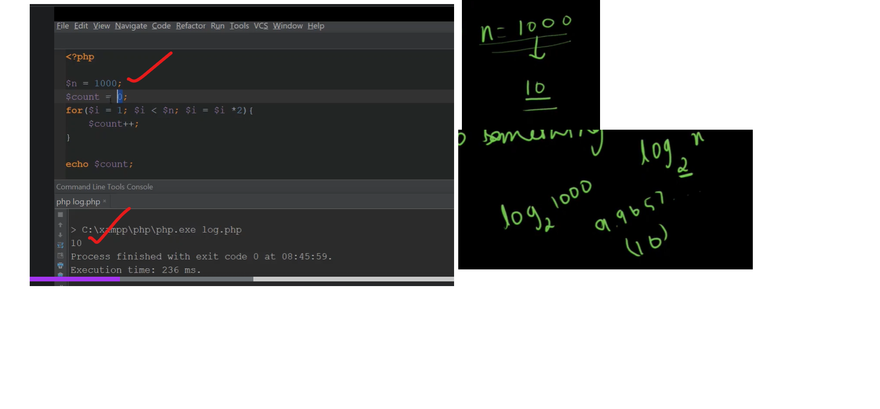
O(logN)

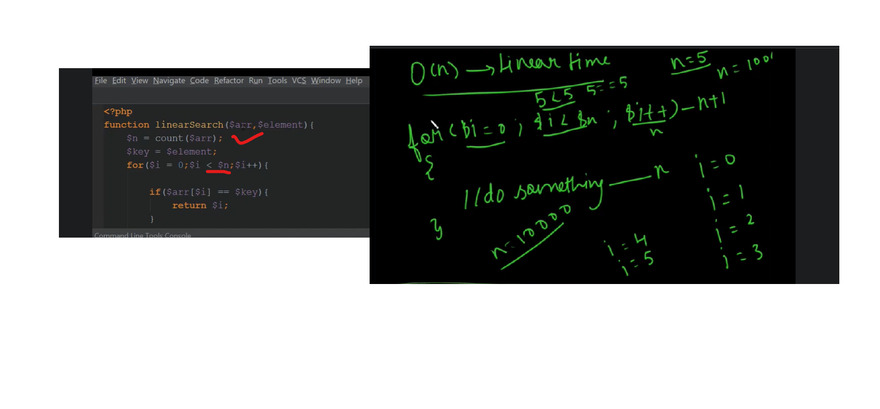
O(N)

public int func(int[] arr) {
    for (int i = 1; i <= arr.length; i++) {
        System.out.println(i);
    }
}

O(N)
describes an algorithm whose runtime will increase linearly relative to the input N

values stored in the array. For example, if the array length is 1, the function will take 1 “step” to run, whereas if the array length is 1000, the function will take 1000 “steps” to run

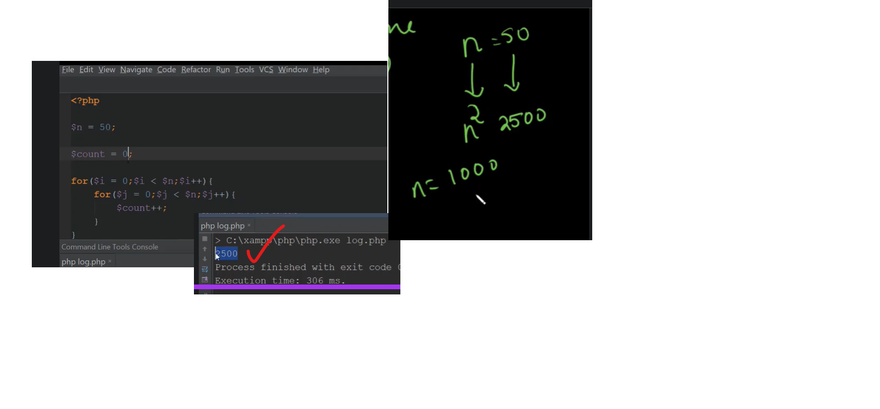
O(N2)

public int func(int[] arr) {
    for (int i = 1; i <= arr.length; i++) {
        for (int i = 1; i <= arr.length; i++) {
        System.out.println(i);
        }
    }
}

O(N2)
describes a function whose runtime is proportional to the square of the input size. This runtime occurs when there is a nested loop such that the outer loop runs N
N times, and the inner loop runs N

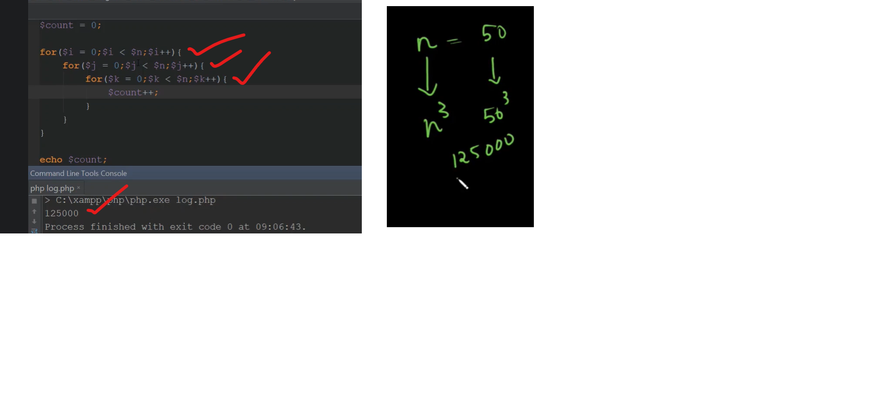
O(N3)