The clustering Algorithms are of many types. The following overview will only list the most prominent examples of clustering algorithms, as there are possibly over 100 published clustering algorithms. Not all provide models for their clusters and can thus not easily be categorized.
Distribution-based methods
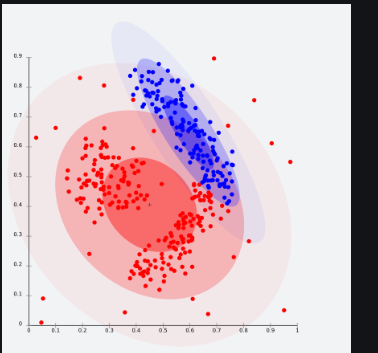
It is a clustering model in which we will fit the data on the probability that how it may belong to the same distribution. The grouping done may be normal or gaussian. Gaussian distribution is more prominent where we have a fixed number of distributions and all the upcoming data is fitted into it such that the distribution of data may get maximized. This result in grouping is shown in the figure:
This model works well on synthetic data and diversely sized clusters. But this model may have problems if the constraints are not used to limit the model’s complexity. Furthermore, Distribution-based clustering produces clusters that assume concisely defined mathematical models underlying the data, a rather strong assumption for some data distributions.
For Ex- The expectation-maximization algorithm which uses multivariate normal distributions is one of the popular examples of this algorithm.
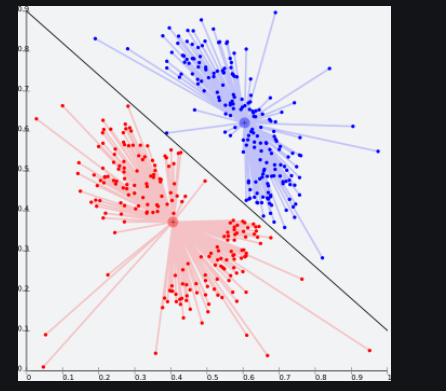
Centroid-based methods
This is basically one of the iterative clustering algorithms in which the clusters are formed by the closeness of data points to the centroid of clusters. Here, the cluster center i.e. centroid is formed such that the distance of data points is minimum with the center. This problem is basically one of the NP-Hard problems and thus solutions are commonly approximated over a number of trials.
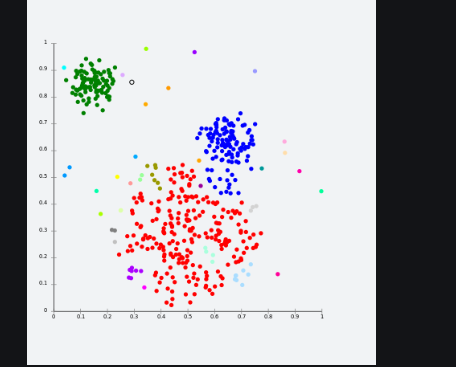
Connectivity based methods :
The core idea of the connectivity-based model is similar to Centroid based model which is basically defining clusters on the basis of the closeness of data points. Here we work on a notion that the data points which are closer have similar behavior as compared to data points that are farther.
It is not a single partitioning of the data set, instead, it provides an extensive hierarchy of clusters that merge with each other at certain distances. Here the choice of distance function is subjective. These models are very easy to interpret but it lacks scalability.
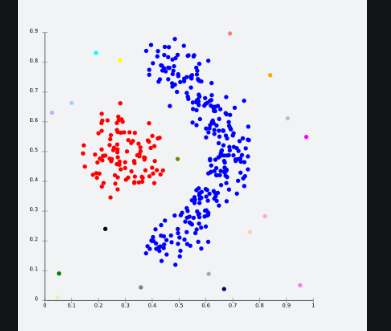
Density Models: In this clustering model, there will be searching of data space for areas of the varied density of data points in the data space. It isolates various density regions based on different densities present in the data space.
For Ex- DBSCAN and OPTICS.
Which type of clustering algorithm is used to use clustering
Each type of clustering algorithm—hierarchical, density-based, centroid-based, and distribution-based—has its own strengths and weaknesses, making them suitable for different types of data and clustering objectives. Here's when each type of clustering algorithm is typically suitable:
Hierarchical Clustering
Suitable Cases:
When the hierarchy or structure of the clusters is important and needs to be visualized.
When there is no predefined number of clusters, and you want to explore the data at different levels of granularity.
Advantages:
Provides a hierarchical structure of clusters, allowing users to understand relationships at different levels of detail.
No need to specify the number of clusters in advance.
Disadvantages:
Can be computationally expensive, especially for large datasets.
May not be suitable for very large datasets due to scalability issues.
Density-Based Clustering (e.g., DBSCAN, OPTICS):
Suitable Cases:
When dealing with datasets containing noise and outliers.
When clusters have irregular shapes and varying densities.
Advantages:
Can detect clusters of arbitrary shapes.
Robust to noise and outliers.
Disadvantages:
Requires tuning of parameters such as the minimum number of points and the neighborhood size.
May struggle with datasets of varying densities.
Centroid-Based Clustering (e.g., K-means, K-medoids):
Suitable Cases:
When the number of clusters is known or can be estimated.
When clusters are well-separated and roughly spherical in shape.
Advantages:
Computationally efficient and scalable to large datasets.
Easy to interpret and implement.
Disadvantages:
Sensitive to the initial selection of centroids.
May produce suboptimal results if clusters have different sizes or non-spherical shapes.
Distribution-Based Clustering (e.g., Gaussian Mixture Models):
Suitable Cases:
When clusters are assumed to follow certain probability distributions (e.g., Gaussian distributions).
When clusters overlap and cannot be easily separated in the feature space.
Advantages:
Can capture complex data distributions and overlapping clusters.
Provides probabilistic cluster assignments.
Disadvantages:
May require knowledge of the underlying data distribution.
Sensitive to the choice of the number of components in the mixture model.

Top comments (0)