Dimensionality reduction
curse of dimensionality
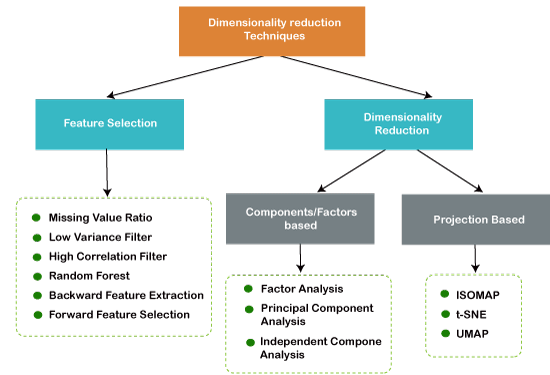
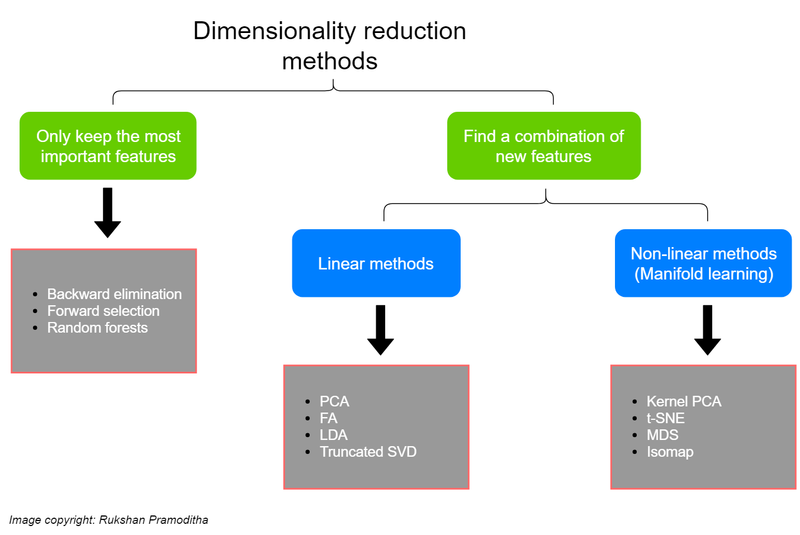
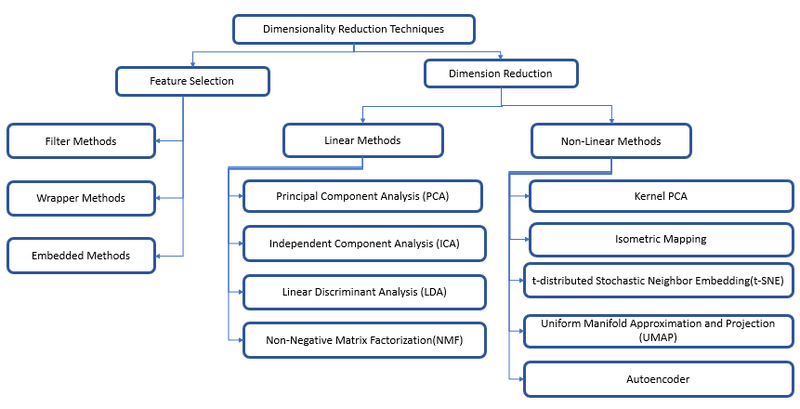
Dimensionality reduction is a technique used in machine learning and data analysis to reduce the number of input variables (features or dimensions) in a dataset while preserving important information. It is commonly employed to address issues related to the curse of dimensionality, reduce computational complexity, and improve the performance of machine learning models. Two popular dimensionality reduction techniques are Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE).
Let's explain PCA with an example:
Principal Component Analysis (PCA):
PCA is a linear dimensionality reduction technique that aims to find a lower-dimensional representation of a dataset while retaining as much variance as possible. It achieves this by identifying the principal components (orthogonal linear combinations of the original features) that capture the most significant variability in the data.
Here's an example of PCA using Python's scikit-learn library:
import numpy as np
from sklearn.decomposition import PCA
# Create a sample dataset with three features
data = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]])
# Instantiate the PCA model with two components
pca = PCA(n_components=2)
# Fit the model and transform the data to the lower-dimensional space
transformed_data = pca.fit_transform(data)
# Print the transformed data
print("Transformed Data (2 Principal Components):")
print(transformed_data)
In this example, we create a sample dataset with three features and apply PCA to reduce it to two principal components. The transformed data retains most of the variance from the original dataset while reducing the dimensionality.
The output would look like:
Transformed Data (2 Principal Components):
[[-5.74456265e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00]
[ 5.74456265e+00 0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00]]
In this transformed data, the second principal component captures almost no variance, indicating that it is less informative. By reducing the dataset's dimensionality, PCA simplifies the data while preserving the most critical information, making it easier to analyze or feed into machine learning models.
PCA is widely used in various fields, such as image processing, feature engineering, and data visualization, to reduce dimensionality and improve computational efficiency without sacrificing important information.
Why we use Dimensionality reduction techniques
Dimensionality reduction techniques are used for several important reasons in machine learning and data analysis:
Curse of Dimensionality: As the number of features (dimensions) in a dataset increases, the amount of data required to accurately model and analyze that dataset grows exponentially. High-dimensional data can lead to increased computational complexity, longer training times, and overfitting. Dimensionality reduction helps mitigate the curse of dimensionality by reducing the number of features while retaining essential information.
Improved Model Performance: In many cases, high-dimensional data can lead to models that perform poorly due to noise or redundancy in the features. Dimensionality reduction can help improve model performance by eliminating irrelevant or redundant features, which can lead to simpler and more interpretable models.
Visualization: Visualizing high-dimensional data is challenging. Reducing data to a lower-dimensional space allows for effective data visualization, making it easier to explore and understand the data's structure, patterns, and relationships. Techniques like PCA and t-SNE are commonly used for data visualization.
Computational Efficiency: Training machine learning models with a large number of features can be computationally expensive. Reducing dimensionality can significantly speed up the training process, making it more feasible to work with complex models or large datasets.
Overcoming Multicollinearity: In some datasets, features are highly correlated or exhibit multicollinearity. This can lead to unstable model coefficients and difficulties in interpreting feature importance. Dimensionality reduction techniques can help reduce collinearity by transforming features into uncorrelated components.
Noise Reduction: High-dimensional datasets may contain noisy or irrelevant features that can negatively impact model performance. Dimensionality reduction can help filter out noise by focusing on the most informative features.
Feature Engineering: Feature engineering is a crucial step in machine learning. Dimensionality reduction can be part of feature engineering, helping to create more meaningful and informative features by combining or transforming the original features.
Reducing Storage Requirements: In some applications, reducing the dimensionality of data can lead to significant savings in storage space, especially when dealing with large datasets.
Interpretability: Simplifying the dataset by reducing dimensionality can lead to more interpretable models. It's easier to understand and explain the importance of a few key features compared to many.
Preprocessing for Other Techniques: Dimensionality reduction can be a preprocessing step for other machine learning techniques, such as clustering or anomaly detection. Reducing dimensionality often helps these techniques perform better.
Overall, dimensionality reduction is a valuable tool for improving the efficiency, interpretability, and generalization performance of machine learning models, particularly when dealing with high-dimensional data. However, it should be applied carefully, as information loss is inherent in the process, and the choice of the right technique and the number of dimensions to retain should be based on the specific problem and domain knowledge.
Real time application of dimensionality reduction technique
Dimensionality reduction techniques find real-time applications in various domains where high-dimensional data is prevalent. Here are some real-time applications of dimensionality reduction:
Image and Video Processing:
Application: Image and video analysis, object recognition, and compression.
Use Case: Principal Component Analysis (PCA) or autoencoders can be used to reduce the dimensionality of image and video data, making processing and analysis more efficient. For example, facial recognition systems often use dimensionality reduction techniques.
Natural Language Processing (NLP):
Application: Text classification, sentiment analysis, and topic modeling.
Use Case: Reducing the dimensionality of text data using techniques like Latent Semantic Analysis (LSA) or t-Distributed Stochastic Neighbor Embedding (t-SNE) can help uncover hidden patterns and improve the efficiency of NLP tasks.
Bioinformatics:
Application: Genomic data analysis and biomarker discovery.
Use Case: Dimensionality reduction is applied to high-dimensional biological data to identify important genes, classify diseases, and discover patterns in gene expression data.
Recommendation Systems:
Application: Product recommendations in e-commerce, content recommendations in streaming platforms.
Use Case: Collaborative filtering techniques often employ dimensionality reduction to reduce the feature space and find similarities between users or items efficiently.
Sensor Data Analysis:
Application: Internet of Things (IoT) and sensor networks for monitoring and anomaly detection.
Use Case: Dimensionality reduction helps reduce noise and extract meaningful features from sensor data, enabling real-time detection of anomalies or patterns in data streams.
Finance and Stock Market Analysis:
Application: Predictive modeling, risk assessment, and algorithmic trading.
Use Case: Dimensionality reduction can be used to analyze and model financial time series data by reducing noise and identifying relevant features for forecasting stock prices or assessing portfolio risk.
Healthcare:
Application: Medical imaging, disease diagnosis, and patient monitoring.
Use Case: Dimensionality reduction techniques are applied to medical imaging data, such as MRI or CT scans, to extract relevant features for diagnosis and visualization.
Speech Recognition:
Application: Voice assistants, transcription services.
Use Case: Dimensionality reduction can simplify acoustic modeling and reduce computational complexity in speech recognition systems, making them more responsive in real-time applications.
Quality Control in Manufacturing:
Application: Identifying defects and ensuring product quality.
Use Case: Dimensionality reduction helps process sensor data from manufacturing systems, enabling real-time quality control and defect detection.
Social Media Analysis:
Application: Sentiment analysis, user profiling, and trend detection.
Use Case: Reducing dimensionality in social media data can aid in identifying influential users, tracking trends, and improving recommendation systems for real-time content delivery.
curse of dimensionality
The "curse of dimensionality" is a term used in machine learning and statistics to describe the problems and challenges that arise when working with high-dimensional data, particularly in spaces with many features or dimensions. It refers to the exponential increase in data volume as the number of dimensions (features) grows, which can lead to various issues. Let's explain the curse of dimensionality with an example:
Example: Curse of Dimensionality in Machine Learning
Suppose you are working on a classification problem where you want to predict whether an email is spam or not. You decide to use a machine learning algorithm to build a spam filter. Initially, you consider using the following features for each email:
Length of the email (number of words)
Number of unique words
Presence or absence of specific keywords (binary flags)
Number of links in the email
Number of images in the email
Number of attachments
Number of misspelled words
Presence or absence of certain patterns or characters
As you collect data and engineer more features, the dimensionality of your dataset grows. Let's say you end up with 100 features for each email.
Now, here's how the curse of dimensionality can manifest in this scenario:
Data Sparsity: As the number of dimensions increases, the amount of data needed to adequately represent the feature space also increases exponentially. In high-dimensional spaces, data points become sparse, meaning there are fewer data points relative to the number of dimensions. This sparsity can make it challenging to find meaningful patterns in the data.
Increased Computational Complexity: High-dimensional data requires more computational resources to process. Many machine learning algorithms, particularly distance-based algorithms like k-nearest neighbors (KNN) or clustering methods, become less efficient and more computationally intensive in high dimensions. This can lead to longer training times and increased memory usage.
Overfitting: With a large number of features, the risk of overfitting the model to noise in the data increases. Overfitting occurs when the model captures the noise in the training data rather than the underlying patterns. High-dimensional spaces make it easier for models to find spurious correlations that don't generalize well to new, unseen data.
Diminished Discriminative Power: In high-dimensional spaces, data points tend to be equidistant from each other. This equidistance can lead to poor discrimination between classes, as it becomes challenging to find meaningful boundaries or decision boundaries that separate the classes effectively.
To mitigate the curse of dimensionality, you may consider:
Feature selection techniques to choose the most relevant features.
Dimensionality reduction methods like Principal Component Analysis (PCA) or t-Distributed Stochastic Neighbor Embedding (t-SNE) to reduce the number of dimensions.
Collecting more data if possible to reduce sparsity.
Using algorithms designed to handle high-dimensional data efficiently, like tree-based methods (e.g., Random Forests) or linear models (e.g., Logistic Regression).
In summary, the curse of dimensionality is a critical consideration in machine learning because it can impact the performance, efficiency, and interpretability of models when dealing with high-dimensional data. Careful feature engineering and dimensionality reduction can help address these challenges.

Top comments (0)