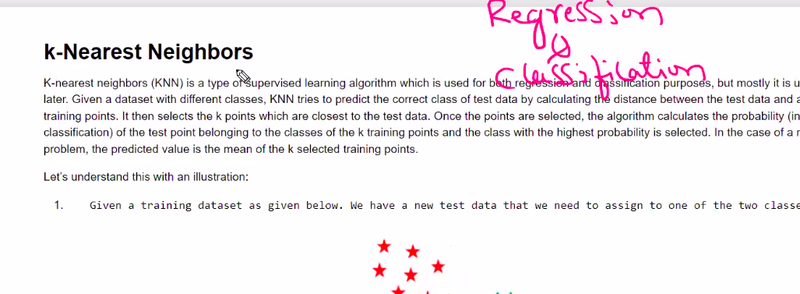
What is knn
On what basis k value selects in Machine learning
what are the method to find distance between data set and k value
why knn is Lazy learners
When knn should apply in Ml
What is knn
In k-nearest neighbors (KNN) algorithm, the value of k is a hyperparameter that you need to choose before training the model. It greatly influences the performance and behavior of the KNN algorithm. The selection of the appropriate k value is essential to ensure the best performance of the model. Here are some common approaches to select the k value:
On what basis k value selects in Machine learning
In k-nearest neighbors (KNN) algorithm, the value of k is a hyperparameter that you need to choose before training the model. It greatly influences the performance and behavior of the KNN algorithm. The selection of the appropriate k value is essential to ensure the best performance of the model. Here are some common approaches to select the k value:
Cross-Validation: Divide your dataset into multiple folds and perform cross-validation. For each fold, train the KNN model with different values of k and measure the performance (e.g., accuracy, F1 score, etc.). Choose the k value that gives the best average performance across all folds.
Odd Numbers: In binary classification problems, it is a good practice to choose an odd number for k to avoid ties when voting. Ties can cause confusion in deciding the final class label for a data point.
Square Root of N: A simple rule of thumb is to set k to the square root of the number of data points in your dataset. This approach provides a balance between overfitting (low k values) and underfitting (high k values).
Elbow Method: Plot the performance metric (e.g., accuracy) against different values of k. Look for a point on the graph where increasing k no longer significantly improves the performance. This point is often referred to as the "elbow" and can be a good k value to choose.
Domain Knowledge: If you have some prior knowledge about the problem domain or the nature of the data, you can use that information to select an appropriate k value.
Grid Search: Perform an exhaustive search over a predefined range of k values and evaluate the model performance for each k. Choose the k value that gives the best results.
It's important to note that the choice of k should be influenced by the characteristics of your data. Smaller values of k (e.g., 1 or 3) can lead to a more flexible and locally sensitive model but may be prone to noise or outliers. On the other hand, larger values of k can lead to a smoother decision boundary and can be more robust to noise, but they may not capture the local patterns well.
Remember, there is no one-size-fits-all answer for the best k value; it depends on the specific dataset and problem at hand. Experimenting with different values of k and evaluating the performance on validation sets will help you find the most suitable k value for your KNN model.
what are the method to find distance between data set and k value
To find the distance between data points and determine the appropriate k value in machine learning, you typically use distance metrics and validation techniques. Here are the main methods:
Distance Metrics:
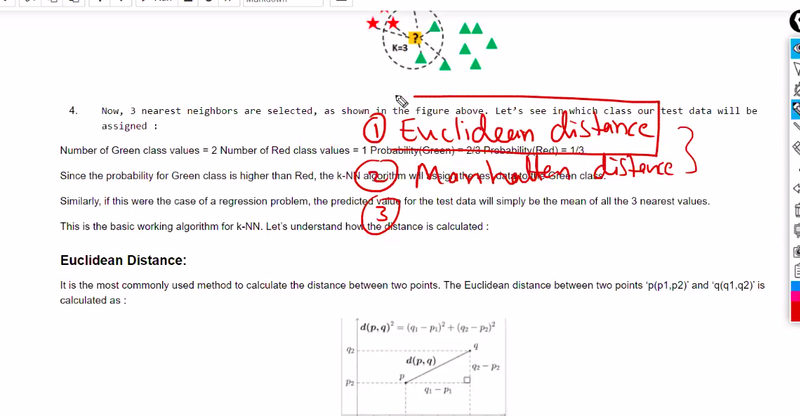
Euclidean Distance: The most common distance metric used in KNN. It calculates the straight-line distance between two data points in a multidimensional space.
Manhattan Distance: Also known as the L1 norm, it calculates the sum of absolute differences between the coordinates of two data points.
Minkowski Distance: A generalization of both Euclidean and Manhattan distances. It includes a parameter 'p', allowing you to control the distance calculation (Euclidean distance is a special case when p=2).
Cosine Similarity: Measures the cosine of the angle between two data vectors, often used for text data or high-dimensional sparse data.
Grid Search and Cross-Validation for K value:
Grid Search: Define a range of possible k values and then train the KNN model using each k value. Evaluate the performance of the model (e.g., using cross-validation) for each k value and select the one that gives the best results.
Cross-Validation: Split your dataset into training and validation sets. Then, use techniques like k-fold cross-validation to evaluate the model's performance for different k values on multiple train-validation splits. This helps you choose the most suitable k value that generalizes well to unseen data.
Elbow Method:
As mentioned earlier, plot the performance metric (e.g., accuracy) against different k values. Look for the "elbow" point on the graph, which is the point where increasing k no longer significantly improves the performance. This can be a good k value to choose.
Domain Knowledge:
Depending on the nature of your data and the problem you are solving, you might have some domain knowledge that suggests a reasonable k value. For example, if you are dealing with spatial data and have some understanding of the neighborhood sizes, it can guide you in choosing k.
Model Complexity vs. Generalization Trade-off:
Smaller values of k lead to more complex models that are sensitive to noise and local fluctuations in the data.
Larger values of k lead to smoother decision boundaries and more robust models but might miss local patterns in the data.
Balancing this trade-off is crucial, and it can be achieved by experimenting with different k values and observing their impact on the model's performance.
Remember that the choice of distance metric and k value can significantly impact the performance of your KNN model. Therefore, it's essential to experiment with different configurations and validate your choices using proper evaluation techniques to select the best k value for your specific machine learning problem.
why knn is Lazy learners
Lazy learners, also known as instance-based learners, are a type of machine learning algorithm that does not learn an explicit model during training. Instead, they memorize the training data and use it to make predictions for new, unseen instances. These algorithms store the entire training dataset in memory and perform the majority of their computations during the prediction phase.
The key characteristics of lazy learners include:
No Explicit Training Phase: Lazy learners do not have a traditional training phase where they learn a model based on the training data. Instead, they directly use the training data to make predictions.
Instance-Based Decision Making: When a new instance needs to be classified, lazy learners look for the most similar instances in the training data (based on a distance metric) and use the labels of those instances to make predictions.
Lazy Evaluation: The actual computation and decision-making happen at the time of prediction, rather than during training. This can be computationally more expensive during prediction, especially for large datasets.
Flexible to Training Data: Since lazy learners memorize the training data, they can adapt quickly to changes in the dataset or new data points without needing to retrain the model.
Interpretable: Lazy learners are often more interpretable than eager learners (e.g., models like decision trees or neural networks) because they directly use instances from the training data to make predictions.
Examples of lazy learner algorithms include:
k-Nearest Neighbors (KNN): A classic lazy learning algorithm where the class of an unseen data point is determined by the majority class of its k-nearest neighbors in the feature space.
Locally Weighted Learning (LWL): A variation of KNN that assigns different weights to the neighboring points based on their distance to the query point.
Radial Basis Function Networks (RBFN): These networks use a radial basis function to measure the similarity between instances and perform classification based on these similarities.
Case-Based Reasoning (CBR): A lazy learning approach that uses past experiences (cases) to solve new problems by finding the most similar cases and adapting their solutions.
Lazy learners can be effective for certain types of problems, especially when the decision boundary is complex and difficult to model explicitly. However, they can also be computationally expensive during prediction, especially for large datasets, and might not perform well if the training data is noisy or high-dimensional. As with any machine learning algorithm, it's important to consider the characteristics of the data and problem domain when choosing between lazy learners and eager learners (which have a traditional training phase followed by a separate prediction phase).
Yes, that's correct! k-Nearest Neighbors (KNN) is a prime example of a lazy learner in machine learning. As mentioned earlier, lazy learners are instance-based algorithms that memorize the entire training dataset and make predictions for new data points based on the similarity to the existing data instances.
In the case of KNN:
No Training Phase: KNN does not have an explicit training phase where it learns a model from the training data. Instead, it directly uses the training data to make predictions.
Instance-Based Decision Making: When presented with a new, unseen data point, KNN looks for the k-nearest neighbors (k data points with the smallest distances) to the new instance in the feature space. The class of the new data point is determined by the majority class of its k-nearest neighbors.
Lazy Evaluation: The actual computation in KNN occurs during prediction when it identifies and compares the distances of the new instance with the training instances to find the nearest neighbors.
Flexible to Training Data: KNN can adapt quickly to changes in the dataset or the addition of new data points without requiring a retraining process. The model is updated on the fly by simply adding the new instances to the existing dataset.
KNN is widely used for classification and regression tasks and is simple to implement. However, it has some limitations, such as being sensitive to the choice of distance metric, becoming computationally expensive for large datasets, and struggling with high-dimensional data. It also doesn't provide an explicit model representation like other algorithms (eager learners), making it less interpretable.
When Knn should apply in Ml
K-nearest neighbors (KNN) is a versatile and useful algorithm that can be applied in various machine learning scenarios. It works well in certain situations and is commonly used for specific types of problems. Here are some scenarios where KNN is particularly suitable:
Classification Problems: KNN is primarily used for classification tasks, where the goal is to assign a class label to a data point based on its neighbors' class labels. It works well for problems with well-defined local decision boundaries and where the class distribution is not highly imbalanced.
Small to Medium-Sized Datasets: KNN's lazy learning approach allows it to handle small to medium-sized datasets efficiently. Since it doesn't require an explicit training phase, it can quickly adapt to new data points without costly model retraining.
Non-Linear Decision Boundaries: KNN can effectively capture non-linear decision boundaries, especially when the data distribution is complex and not easily separable using linear models.
Noise Handling: KNN can be robust to noisy data because it takes into account multiple neighbors for decision-making. Outliers are less likely to influence the overall prediction.
Multi-Class Classification: KNN can handle multi-class classification problems naturally without the need for modifications.
Feature Engineering: KNN can be helpful in feature engineering and data exploration, as it allows you to identify instances that are similar or dissimilar to a given data point based on the distance metric.
Recommender Systems: KNN can be used in collaborative filtering-based recommender systems to find similar users or items based on their interactions or attributes.
Anomaly Detection: KNN can be used for anomaly detection by identifying data points that are significantly different from their neighbors.
However, there are some scenarios where KNN may not be the best choice:
Large Datasets: As KNN requires computing distances between data points, it can become computationally expensive and memory-intensive for large datasets. Approximate nearest neighbor techniques are sometimes used to mitigate this issue.
High-Dimensional Data: In high-dimensional spaces, the concept of "nearest neighbors" can become less meaningful due to the curse of dimensionality, where distances between data points tend to become more uniform, making KNN less effective.
Imbalanced Datasets: KNN can be biased toward the majority class in imbalanced datasets, leading to poorer performance on minority classes. Techniques like resampling or using different distance weights can be applied to address this.
Data Preprocessing: KNN is sensitive to the scale of features, so it's important to perform proper feature scaling and data normalization before applying KNN.
In summary, KNN is a simple and powerful algorithm, particularly well-suited for smaller datasets with well-defined local structures and non-linear decision boundaries. It can be a useful tool in the data scientist's toolkit when applied appropriately and with consideration of its strengths and limitations.
Some Important Points and Objective Question
knn is supervised learning
used for both regression and classification
multiple classification but logistic regression is used for binary classification
Task
predict correct class of test data
calculate distance b/w test data and all training points
on what basis k value select
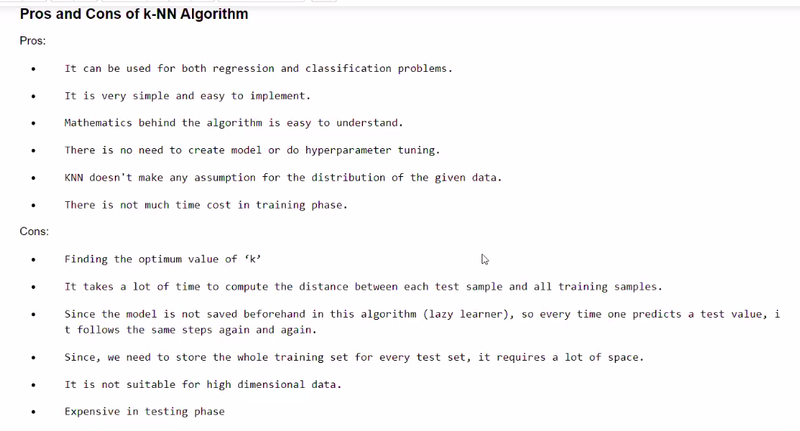
Objective==pros and cons of knn
on what basis k value select
cross validation,odd no,square method,Elbow method
Domain knowledge,Grid search
pros and cons of smaller and larger value of k
what are the method to find distance between dataset and k value
--Euclidian distance,minkowski disatce,cosine similarity,grid search,elbow method,cross validation
Why knn is lazy learner-points see
Example of lazy learner algo=see points
When knn should apply in ml
When knn should not apply
knn used to find distance between---- and -------
knn---calculates the probabilty between
New terms to read and research
Minkowski Distance
Cosine Similarity
Locally Weighted Learning (LWL)
Radial Basis Function Networks (RBFN)
Case-Based Reasoning (CBR)
Anomaly Detection
Recommender Systems





Top comments (0)