Explain structure of neural network

How Do Neural Networks Work
What is the role of weight, bias and hidden layer
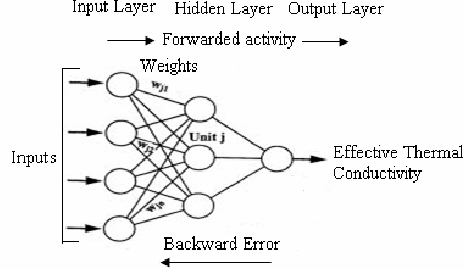
difference between single layer feed-forward network and Multilayer recurrent network.

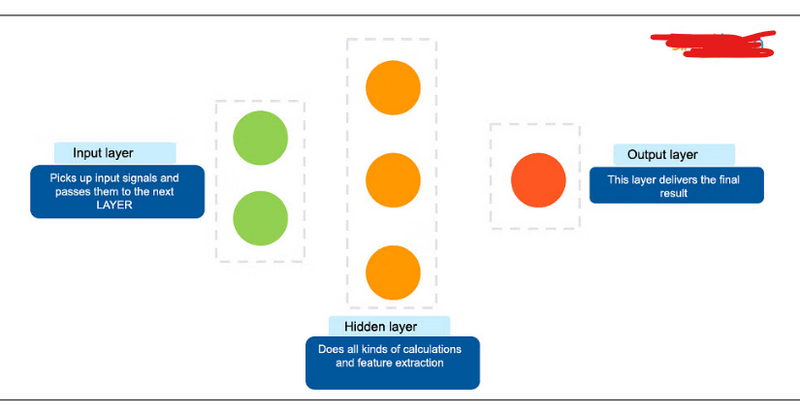
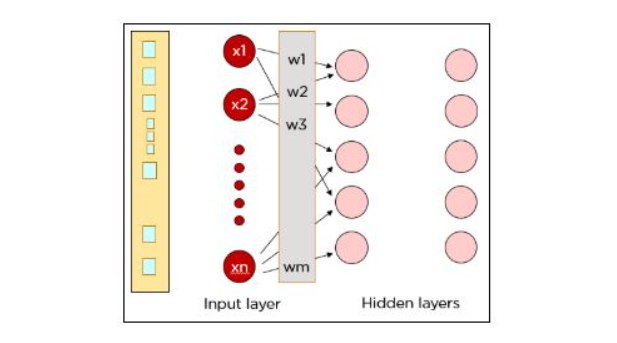
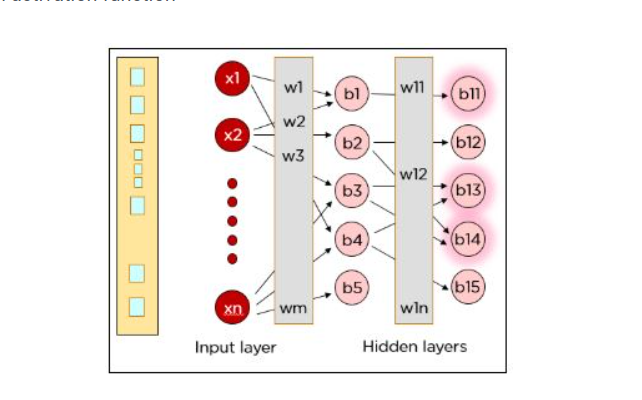
A neural network is usually described as having different layers. The first layer is the input layer, it picks up the input signals and passes them to the next layer. The next layer does all kinds of calculations and feature extractions—it’s called the hidden layer. Often, there will be more than one hidden layer. And finally, there’s an output layer, which delivers the final result

Working of Neural Network
A neural network is usually described as having different layers. The first layer is the input layer, it picks up the input signals and passes them to the next layer. The next layer does all kinds of calculations and feature extractions—it’s called the hidden layer. Often, there will be more than one hidden layer. And finally, there’s an output layer, which delivers the final result.

Different layers in a Neural Network

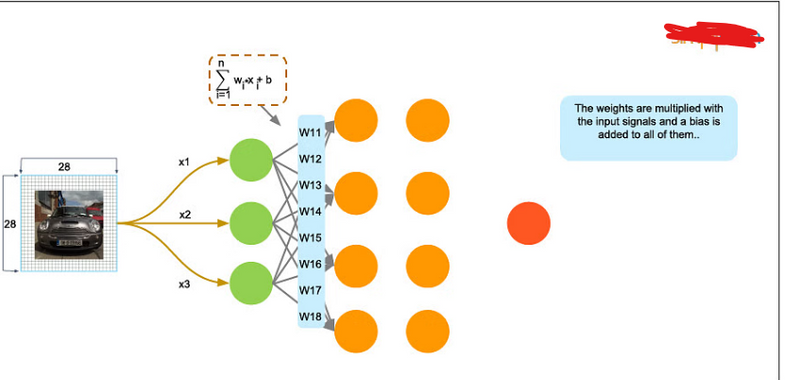
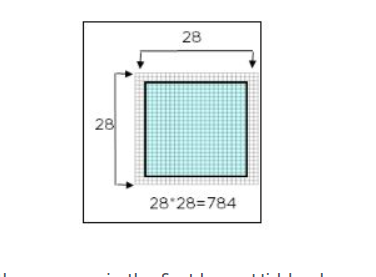
Let’s take the real-life example of how traffic cameras identify license plates and speeding vehicles on the road. The picture itself is 28 by 28 pixels, and the image is fed as an input to identify the license plate. Each neuron has a number, called activation, which represents the grayscale value of the corresponding pixel, ranging from 0 to 1—it’s 1 for a white pixel and 0 for a black pixel. Each neuron is lit up when its activation is close to 1.

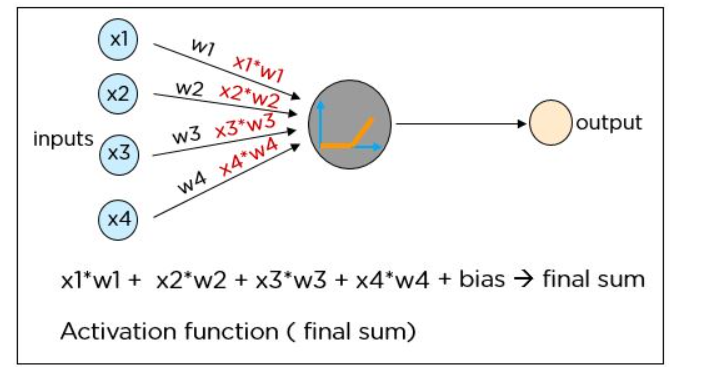
Pixels in the form of arrays are fed into the input layer. If your image is bigger than 28 by 28 pixels, you must shrink it down, because you can’t change the size of the input layer. In our example, we’ll name the inputs as X1, X2, and X3. Each of those represents one of the pixels coming in. The input layer then passes the input to the hidden layer. The interconnections are assigned weights at random. The weights are multiplied with the input signal, and a bias is added to all of them.

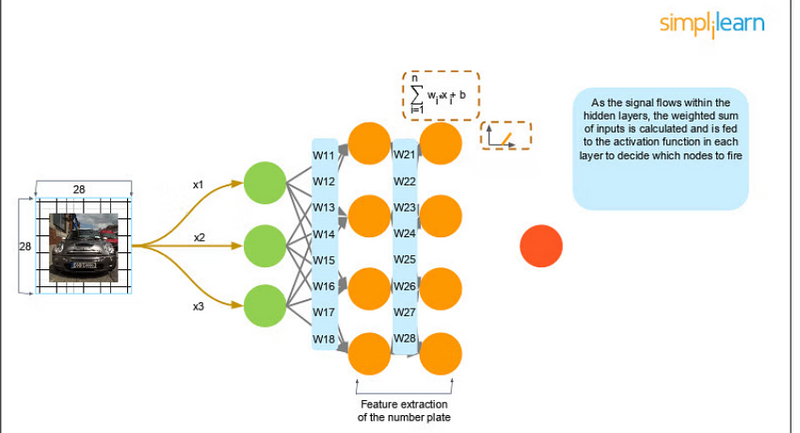
The weighted sum of the inputs is fed as input to the activation function, to decide which nodes to fire for feature extraction. As the signal flows within the hidden layers, the weighted sum of inputs is calculated and is fed to the activation function in each layer to decide which nodes to fire.

Each neuron in a neural network performs the following operations:

1. The product of each input and the weight of the channel it is passed over is found
2. The sum of the weighted products is computed, which is called the weighted sum
3. A bias value of the neuron is added to the weighted sum
4. The final sum is then subjected to a particular function known as the activation function

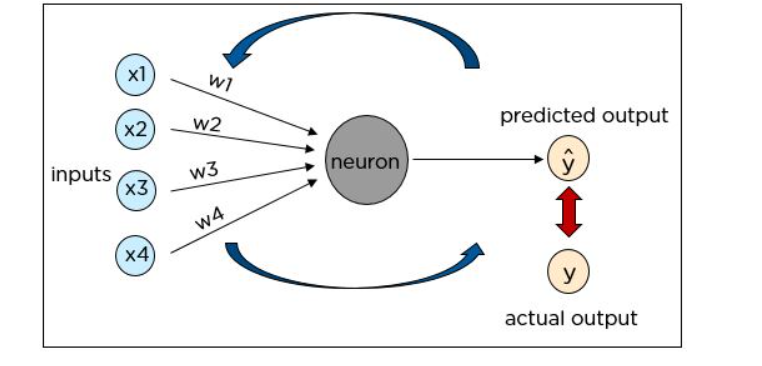
we can not change input value we can change only weight and bias value so that actual value is very close to predicted value

Cost Function
The cost function is one of the significant components of a neural network. The cost value is the difference between the neural nets predicted output and the actual output from a set of labeled training data. The least-cost value is obtained by making adjustments to the weights and biases iteratively throughout the training process.

How Do Neural Networks Work?

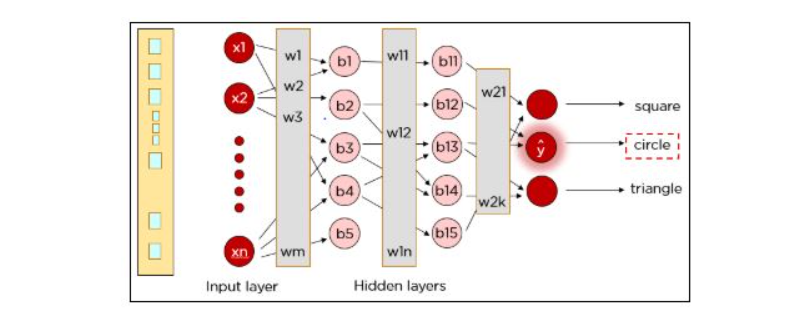
In the next section of this introduction to deep learning the neural network will be trained to identify shapes. The shapes are images of 28*28 pixels.

pixel

Each pixel is fed as input to the neurons in the first layer. Hidden layers improve the accuracy of the output. Data is passed on from layer to layer overweight channels. Each neuron in one layer is weighted to each of the neurons in the next layer.

hidden

Each neuron in the first hidden layer takes a subset of the inputs and processes it. All the inputs are multiplied by their respective weights and a bias is added. The output of the weighted sum is applied to an activation function. The results of the activation function determine which neurons will be activated in the following layer.

Step 1: x1*w1 + x2*w2 + b1

Step 2: Φ(x1* w1 + x2*w2 + b1)

where Φ is an activation function

hidden-layer

The above steps are performed again to ensure the information reaches the output layer, after which a single neuron in the output layer gets activated based on the activation function’s value.

hidden-layers

As you can see, our actual input was a square, but the neural network predicted the output as a circle. So, what went wrong?

The neural network has to be trained until the predicted output is correct and the predicted output is compared to the actual output by calculating the cost function.

The cost function is calculated using the formula where Y is the actual value and Y hat is the predicted value. The cost function determines the error in the prediction and reports it back to the neural network. This is called backpropagation.
The weights are adjusted to reduce the error. The network is trained with the new weights.
Once again, the cost is determined and the backpropagation procedure is continued until the cost cannot be reduced any further.
Similarly, our network can be trained to predict circles and triangles too.
Now that you have a good understanding of how neural networks work, let’s look at some of the important deep learning platforms.

In a neural network, weights and biases are crucial components that play a fundamental role in the network's ability to learn and make predictions. They are associated with the connections (synapses) between neurons and are adjusted during the training process to enable the network to approximate complex functions. Let's explore the roles of weights and biases in a neural network with examples:

Weights:

1. Weights are parameters associated with the connections between neurons in a neural network.
2. Each connection has an associated weight, which represents the strength or importance of that connection in determining the output.
3. Weights are learned during training and are adjusted to minimize the error in the network's predictions.
4. The weights control the influence of the input data on the output of a neuron . Example: Consider a simple feedforward neural network with one input layer, one hidden layer, and one output layer. The weights determine how strongly the inputs affect the output. For instance, if the weight of a connection from input feature X1 to the hidden neuron H1 is 0.5, it means that the input X1 has a moderate positive impact on the activation of H1.

Weights in a neural network determine the strength of connections between neurons. They control how much influence the input to a neuron has on its output. Weights are crucial for the network to learn patterns, features, and complex relationships in the data.

Weights Role: The weights associated with each connection between the input neurons (pixels) and hidden neurons determine which pixels are more relevant for distinguishing between cats and dogs. For example, if the weight connecting the "whisker pixels" to a hidden neuron is large, it means the network has learned that whiskers are important for distinguishing cats from dogs

Example: Image Classification

Imagine building a neural network for image classification, where you want to classify images as either "cats" or "dogs." Each pixel in an image can be treated as an input feature, and each neuron in the network corresponds to a different feature or pattern.

Biases:

1. Biases are parameters associated with each neuron in a neural network, except for the input layer.
2. A bias allows a neuron to shift its activation function horizontally, effectively allowing it to have a non-zero output even when the sum of weighted inputs is zero.
3. Biases help in modeling the "bias" or offset in the data, enabling the network to approximate more complex functions.
4. Biases are also learned during training . Example: In the same neural network as above, each hidden and output neuron has an associated bias. If the bias of hidden neuron H1 is -0.2, it means that H1 will activate with a small negative value even if the weighted sum of inputs is close to zero. This allows the network to capture nonlinear relationships in the data.

The mathematical representation of a neuron's output (z) in a neural network is as follows:

z = (w1 * input1) + (w2 * input2) + ... + (wn * inputn) + bias

Here, "w1, w2, ..., wn" represents the weights, "input1, input2, ..., inputn" represents the inputs, and "bias" represents the bias term associated with the neuron.

During the training process, the network uses optimization techniques (e.g., gradient descent) to adjust the weights and biases in such a way that the predicted output becomes closer to the true target value for a given input. This iterative process is how neural networks learn to model complex relationships and make accurate predictions in various tasks, such as image recognition, natural language processing, and more.

Biases in a neural network allow individual neurons to have a non-zero output even when the sum of weighted inputs is zero. They enable the network to capture offsets and shifts in the data, which is essential for modeling complex relationships.

Example: Sentiment Analysis

Consider a sentiment analysis task, where you want to classify movie reviews as "positive" or "negative." Each word in a review can be considered an input feature, and the neurons in the network represent different textual patterns.

Biases Role: The biases associated with each hidden neuron allow them to activate even when the combined input from words is neutral. For example, if a hidden neuron has a bias term that makes it activate slightly for positive words, it can capture positive sentiment in reviews.

hidden layer

The hidden layers in a neural network play a critical role in its ability to model complex and nonlinear relationships within the data. These layers are located between the input layer and the output layer and are where the network learns to extract and represent important features and patterns from the input data. The role of hidden layers can be best explained through examples:

1. Feature Extraction:

Hidden layers are responsible for feature extraction. Each neuron in a hidden layer computes a weighted sum of its inputs and applies an activation function. This process helps the network learn relevant features from the input data.
Example: In image recognition, the hidden layers may learn to detect edges, shapes, textures, and more complex features like object parts or specific patterns.

1. Nonlinearity:

Hidden layers introduce nonlinearity into the network, which is essential for capturing complex relationships that may not be linearly separable.
Example: In natural language processing, the relationships between words and their meanings are highly nonlinear. Hidden layers in a neural network can learn to encode these relationships by creating complex representations of words or phrases.

1. Representation Learning:

Hidden layers enable the network to learn hierarchical representations. Lower layers capture simple features, while higher layers combine these features to represent more abstract concepts.
Example: In deep learning models for speech recognition, lower hidden layers may capture phonemes, while higher layers learn to recognize words and phrases.

1. Dimensionality Reduction:

Hidden layers can perform dimensionality reduction by mapping high-dimensional input data to a lower-dimensional space. This can help simplify the learning task and reduce overfitting.
Example: In image compression, autoencoders use hidden layers to represent high-resolution images with fewer bits by capturing essential information.

1. Task-Specific Features:

Hidden layers can adapt to the specific task. The network learns which features are relevant for a particular task and suppresses less important ones.
Example: In a recommendation system, hidden layers may learn user preferences, item characteristics, and interactions that are essential for making accurate recommendations.

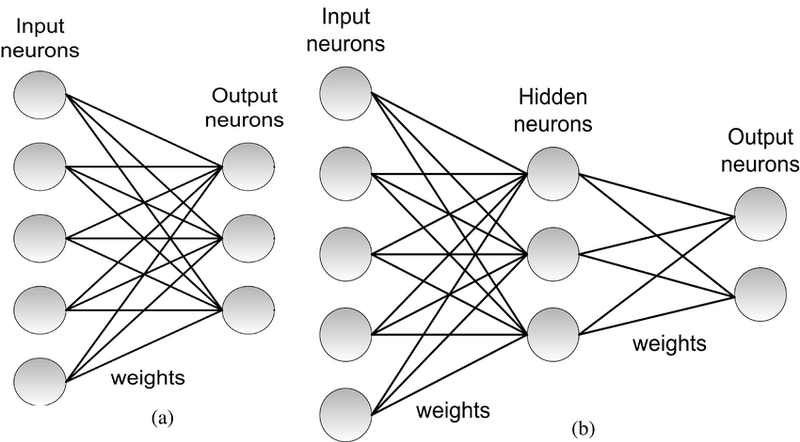
difference between single layer feed-forward network and Multilayer recurrent network

A single-layer feed-forward network and a multilayer recurrent network are two different types of neural network architectures used in machine learning. They have distinct structures and are suitable for different types of tasks. Let's explore the differences between these two types of networks with real examples:

Single-Layer Feed-Forward Network:

Structure:

A single-layer feed-forward network consists of an input layer and an output layer.
It does not contain hidden layers, which means it is a shallow network.
Example:

A classic example of a single-layer feed-forward network is the Perceptron. It can be used for binary classification tasks where the decision boundary is linear.
Example: Classifying whether an email is spam or not based on email features like the number of words and the presence of certain keywords.
Use Case:

Single-layer feed-forward networks are simple and suitable for linearly separable problems.
They are limited in their ability to model complex, nonlinear relationships in data.
Multilayer Recurrent Network (e.g., LSTM or GRU):

Structure:

A multilayer recurrent network, such as a Long Short-Term Memory (LSTM) or Gated Recurrent Unit (GRU), includes multiple hidden layers.
These layers have recurrent connections that allow the network to maintain internal memory and capture sequential dependencies.
Example:

Multilayer recurrent networks are commonly used for sequential data, such as time series prediction, natural language processing, and speech recognition.
Example: Language translation using a sequence-to-sequence LSTM model. It processes one word at a time while maintaining context from previous words.
Use Case:

Multilayer recurrent networks excel at modeling complex, nonlinear relationships in sequential data.
They are capable of handling tasks that require capturing temporal dependencies and long-range context.
Key Differences:

Depth: Single-layer feed-forward networks are shallow networks with no hidden layers, while multilayer recurrent networks consist of multiple hidden layers.

Task Type: Single-layer feed-forward networks are suitable for simple, linearly separable tasks, such as binary classification. Multilayer recurrent networks are designed for sequential data with complex dependencies, including time series analysis, language modeling, and speech recognition.

Memory: Multilayer recurrent networks can capture memory of past events in sequential data, allowing them to maintain context over time, which single-layer feed-forward networks cannot do.

Nonlinearity: Multilayer recurrent networks typically use nonlinear activation functions and recurrent connections to capture complex relationships, while single-layer feed-forward networks use linear or simple activation functions.

Reference