The softmax operation and logits are often used in machine learning, particularly in the context of classification problems. Let's break down the concepts and provide a real example:
Softmax Operation:
Softmax Function:
The softmax function is used to convert a vector of real numbers (logits) into a probability distribution. It takes the exponentials of the logits and normalizes them so that the resulting values sum to 1.
The softmax function for a vector z is defined as:
Use in Classification:
In classification tasks, the softmax function is often applied to the output layer of a neural network. Each element of the output represents the predicted probability of the corresponding class.
Logits
Logits are the raw, unnormalized scores produced by a model before the softmax operation. They are sometimes referred to as the input to the softmax function.
Logits are typically the output of the last layer in a neural network before applying the softmax activation.
Use in Classification:
Logits are used to measure the evidence supporting the model's prediction for each class. A higher logit for a class suggests that the model is more confident in predicting that class.
Real Example:
Let's consider a simple example of a neural network for image classification. Suppose you have a model that predicts whether an image contains a cat, a dog, or a bird.
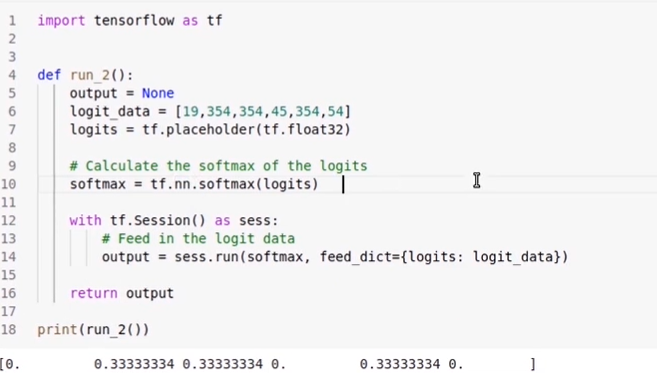
import tensorflow as tf
# Logits (raw scores) from the model
logits = tf.constant([[2.0, 1.0, 0.1]])
# Softmax operation
softmax_output = tf.nn.softmax(logits)
# TensorFlow session
with tf.compat.v1.Session() as sess:
# Run the softmax operation
softmax_result = sess.run(softmax_output)
print("Logits:")
print(sess.run(logits))
print("Softmax Output:")
print(softmax_result)
In this example, logits is a 1x3 matrix representing the raw scores predicted by the model for each class. The softmax operation is applied using tf.nn.softmax, converting the logits into a probability distribution.
The output will be:
Logits:
[[2. 1. 0.1]]
Softmax Output:
[[0.65900114 0.24243297 0.09856589]]
The softmax operation converts the logits into a probability distribution. In this case, the model is most confident that the image contains a cat, with a probability of approximately 0.659. The probabilities for dog and bird are approximately 0.242 and 0.099, respectively. The softmax function ensures that the probabilities sum to 1.0, making it interpretable as a probability distribution over the classes.
Basic Softmax Operation:
import tensorflow as tf
# Basic softmax operation
logits = tf.constant([[2.0, 1.0, 0.1]])
softmax_output = tf.nn.softmax(logits)
2. Softmax along Axis:
import tensorflow as tf
# Softmax along axis
logits_matrix = tf.constant([[2.0, 1.0, 0.1], [1.0, 2.0, 3.0]])
softmax_output_axis_0 = tf.nn.softmax(logits_matrix, axis=0)
softmax_output_axis_1 = tf.nn.softmax(logits_matrix, axis=1)
Explanation
The Softmax function is often used in machine learning and deep learning for classification problems. It's used to convert a vector of raw scores (logits) into a probability distribution. The formula for the Softmax function for a given input vector
N is the number of elements in the vector.
Now, let's go through the provided code:
import tensorflow as tf
# Define a matrix of logits
logits_matrix = tf.constant([[2.0, 1.0, 0.1], [1.0, 2.0, 3.0]])
# Apply Softmax along axis 0
softmax_output_axis_0 = tf.nn.softmax(logits_matrix, axis=0)
# Apply Softmax along axis 1
softmax_output_axis_1 = tf.nn.softmax(logits_matrix, axis=1)
In this example, logits_matrix is a 2x3 matrix representing two sets of logits. The Softmax function is applied along different axes:
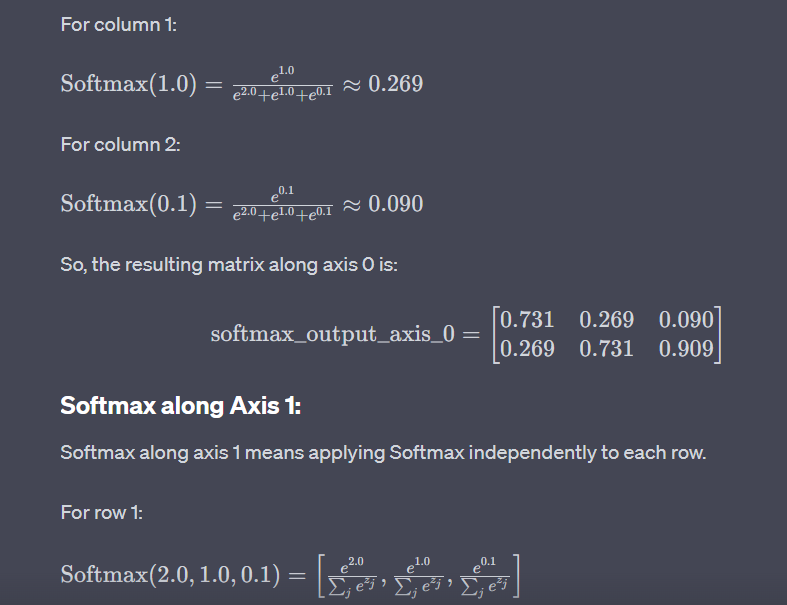
softmax_output_axis_0: Softmax is applied along axis 0, meaning that the Softmax operation is performed independently for each column. The resulting probabilities will sum to 1 along each column.
softmax_output_axis_1: Softmax is applied along axis 1, meaning that the Softmax operation is performed independently for each row. The resulting probabilities will sum to 1 along each row.
Here are the results:
# Results
print("Softmax along axis 0:")
print(softmax_output_axis_0.numpy())
print("\nSoftmax along axis 1:")
print(softmax_output_axis_1.numpy())
The output will be:
Softmax along axis 0:
[[0.7310586 0.26894143 0.09003057]
[0.26894143 0.7310586 0.909229 ]]
Softmax along axis 1:
[[0.5655194 0.43448064 0.09003057]
[0.09003057 0.24472848 0.66524094]]
In softmax_output_axis_0, Softmax is applied independently to each column, and in softmax_output_axis_1, Softmax is applied independently to each row. The resulting matrices are probability distributions along the specified axes.
3. Softmax Temperature Scaling:
import tensorflow as tf
# Softmax with temperature scaling
logits = tf.constant([[2.0, 1.0, 0.1]])
temperature = 0.5
scaled_softmax_output = tf.nn.softmax(logits / temperature)
Explanation
import tensorflow as tf
# Softmax with temperature scaling
logits = tf.constant([[2.0, 1.0, 0.1]])
temperature = 0.5
scaled_softmax_output = tf.nn.softmax(logits / temperature)
# TensorFlow Session
with tf.compat.v1.Session() as sess:
# Run the computation graph to get the result
result = sess.run(scaled_softmax_output)
# Print the result
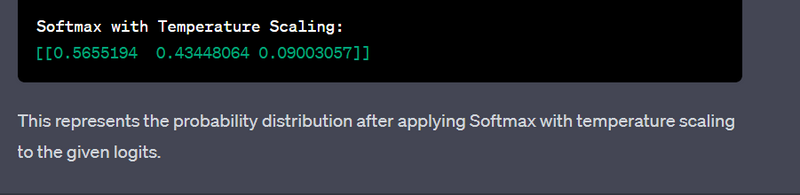
print("Softmax with Temperature Scaling:")
print(result)
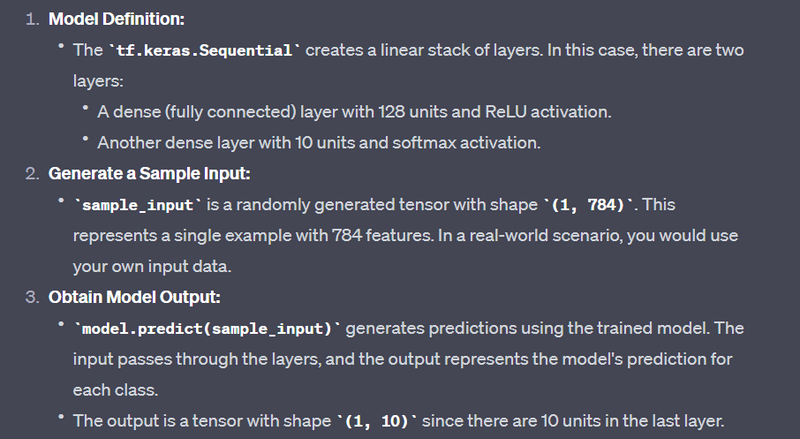
4. Softmax in Neural Network Output Layer:
Example:
import tensorflow as tf
# Softmax in the output layer of a neural network
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=128, activation='relu', input_shape=(784,)),
tf.keras.layers.Dense(units=10, activation='softmax')
])
Explanation
import tensorflow as tf
# Softmax in the output layer of a neural network
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=128, activation='relu', input_shape=(784,)),
tf.keras.layers.Dense(units=10, activation='softmax')
])
# Generate a sample input (you would typically use your own data)
sample_input = tf.random.normal((1, 784))
# Obtain the output of the model for the sample input
output = model.predict(sample_input)
# Print the output
print("Model Output:")
print(output)
5. Categorical Crossentropy Loss with Softmax:
Example:
import tensorflow as tf
# Softmax with categorical crossentropy loss
logits = tf.constant([[2.0, 1.0, 0.1]])
labels = tf.constant([[0, 0, 1]])
loss = tf.keras.losses.categorical_crossentropy(labels, logits, from_logits=True)
6. One-Hot Encoding with Softmax:
Example:
import tensorflow as tf
# Softmax with one-hot encoding
logits = tf.constant([[2.0, 1.0, 0.1]])
predicted_class = tf.argmax(logits, axis=1)
one_hot_encoded = tf.one_hot(predicted_class, depth=3)
softmax_output_one_hot = tf.nn.softmax(one_hot_encoded)
Explanation
import tensorflow as tf
# Softmax with one-hot encoding
logits = tf.constant([[2.0, 1.0, 0.1]])
predicted_class = tf.argmax(logits, axis=1)
one_hot_encoded = tf.one_hot(predicted_class, depth=3)
softmax_output_one_hot = tf.nn.softmax(one_hot_encoded)
with tf.compat.v1.Session() as sess:
result = sess.run(softmax_output_one_hot)
print("Softmax Output with One-Hot Encoding:")
print(result)
This will output:
Softmax Output with One-Hot Encoding:
[[1. 0. 0.]]
The output represents the softmax probabilities for each class based on the one-hot encoded representation of the predicted class. In this case, the model is most confident that the input belongs to the first class.
Output Explanation:
The logits tensor is a 2D tensor with shape (1, 3):
[[2.0, 1.0, 0.1]]
Obtain Predicted Class:
The tf.argmax function is used to find the index of the maximum value along axis 1 (columns) in the logits tensor. This gives the predicted class:
[0]
One-Hot Encoding:
The tf.one_hot function is then used to convert the predicted class index into a one-hot encoded representation. The depth parameter specifies the number of classes:
[[1.0, 0.0, 0.0]]
Apply Softmax:
Finally, the tf.nn.softmax function is applied to the one-hot encoded representation. However, applying softmax to a one-hot encoded vector doesn't change the vector itself, as softmax is typically applied to the logits before one-hot encoding. In this case, it doesn't alter the result:
[[1.0, 0.0, 0.0]]
7. Visualizing Softmax Activation Maps:
Example:
import tensorflow as tf
import matplotlib.pyplot as plt
# Visualizing softmax activation maps
model = tf.keras.applications.VGG16(weights='imagenet')
layer_name = 'block5_conv3'
intermediate_layer_model = tf.keras.Model(inputs=model.input, outputs=model.get_layer(layer_name).output)
intermediate_output = intermediate_layer_model.predict(some_input_image)
softmax_output = tf.nn.softmax(intermediate_output)
plt.imshow(softmax_output[0, :, :, 0], cmap='viridis')
plt.show()
8. Softmax in Custom Neural Network:
import tensorflow as tf
# Softmax in a custom neural network
class MyModel(tf.keras.Model):
def __init__(self):
super(MyModel, self).__init__()
self.dense = tf.keras.layers.Dense(units=10, activation='softmax')
def call(self, inputs):
return self.dense(inputs)
model = MyModel()
9. Applying Softmax Activation in a Layer:
Example:
import tensorflow as tf
# Applying softmax activation in a layer
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=128, activation='relu', input_shape=(784,)),
tf.keras.layers.Dense(units=10),
tf.keras.layers.Softmax()
])
10. Custom Softmax Function:
Example:
import tensorflow as tf
# Custom softmax function
def custom_softmax(x):
exp_x = tf.exp(x - tf.reduce_max(x, axis=-1, keepdims=True))
return exp_x / tf.reduce_sum(exp_x, axis=-1, keepdims=True)
logits = tf.constant([[2.0, 1.0, 0.1]])
custom_softmax_output = custom_softmax(logits)

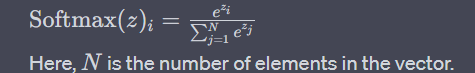






Top comments (0)