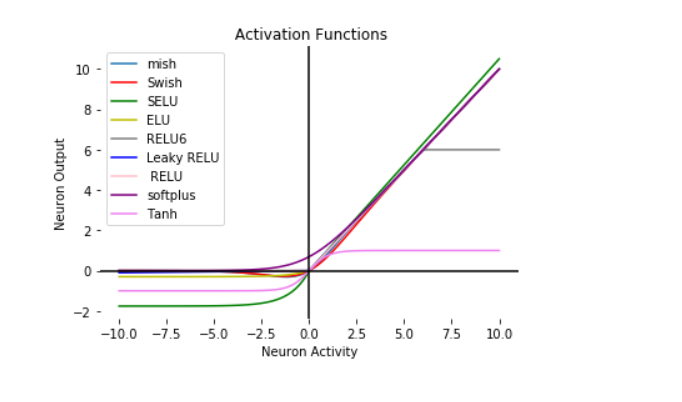
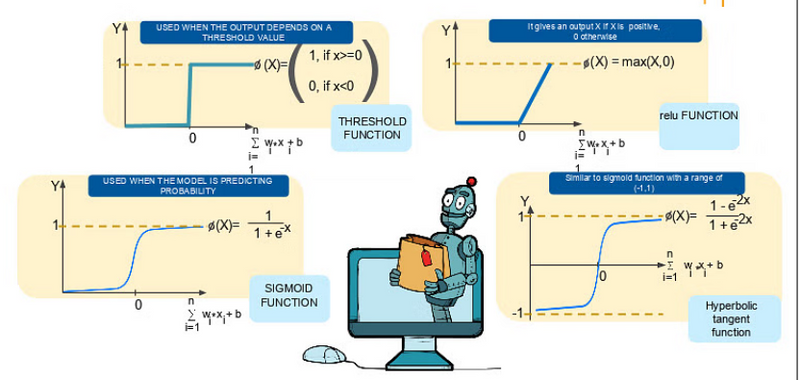
Different type of Activation function
Where to use which activation function
explain the issue or problem in sigmoid and tanh activation function
Difference b/w softmax and sigmoid
Different type of Activation function
Activation functions are essential components in neural networks. They introduce nonlinearity to the network, allowing it to approximate complex functions and learn from data. Different activation functions serve various purposes, and here are some common types with examples:
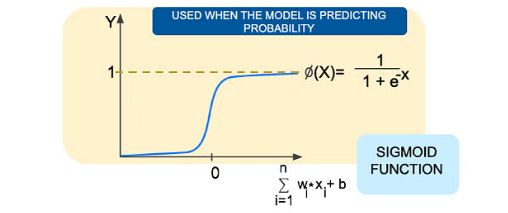
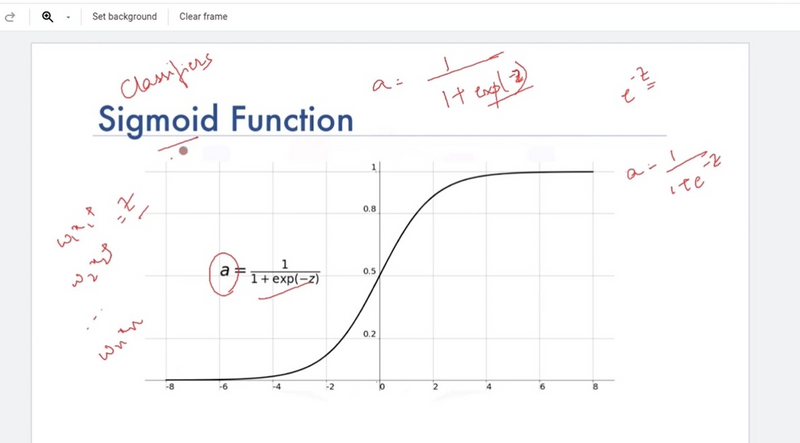
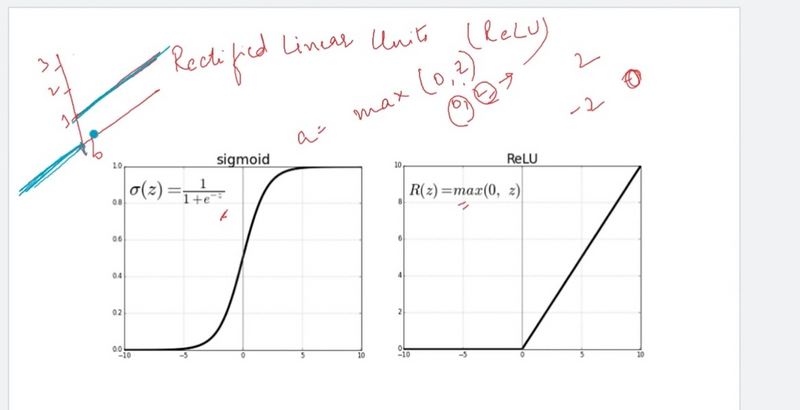
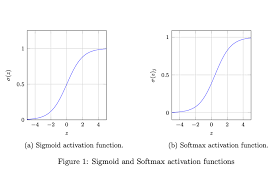
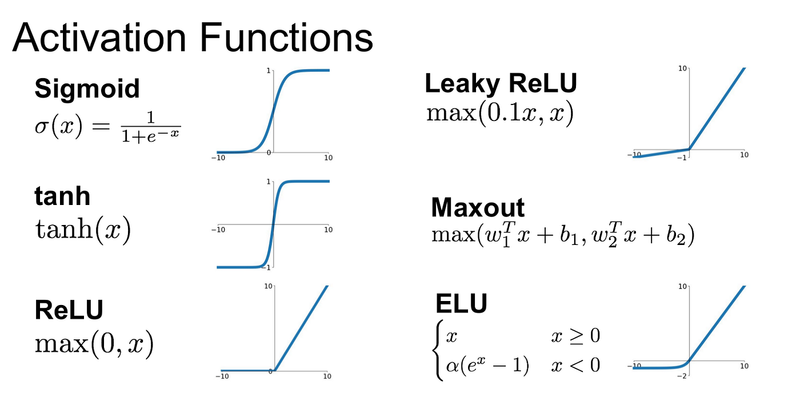
Sigmoid Activation (Logistic):
The sigmoid activation function squashes input values to a range between 0 and 1.
It's often used in the output layer of binary classification problems.
Example:
def sigmoid(x):
return 1 / (1 + np.exp(-x))
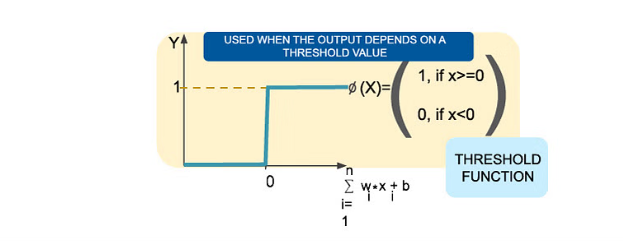
Threshold Function
The threshold function is used when you don’t want to worry about the uncertainty in the middle.
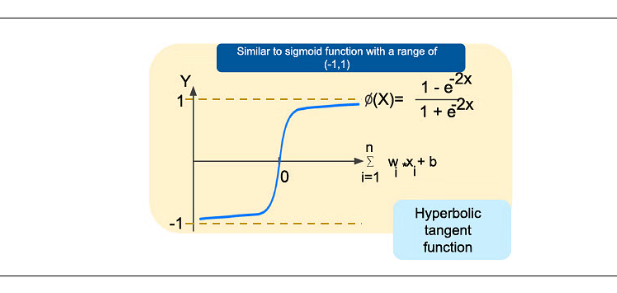
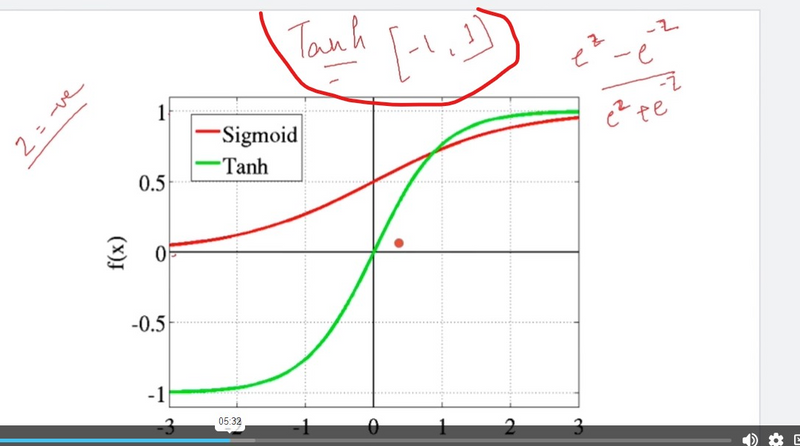
Hyperbolic Tangent (Tanh):
Tanh squashes input values to a range between -1 and 1, making it zero-centered.
It's suitable for hidden layers of neural networks and can handle data with negative values.
Example:
def tanh(x):
return np.tanh(x)
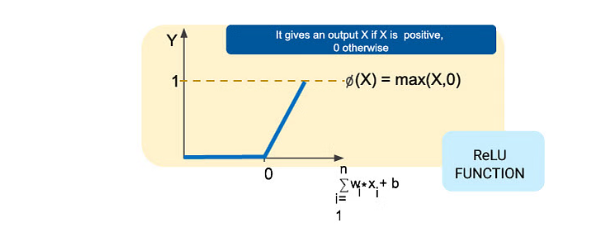
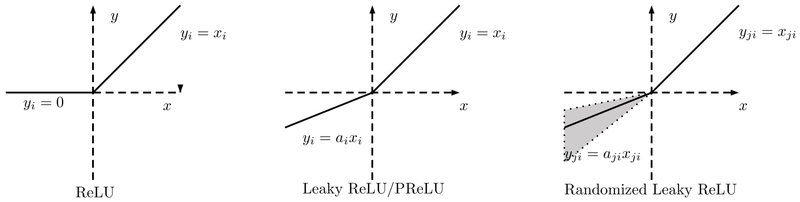
Rectified Linear Unit (ReLU):
ReLU is one of the most popular activation functions. It returns the input for positive values and zero for negative values.
It helps address the vanishing gradient problem and speeds up convergence.
Example:
def relu(x):
return max(0, x)
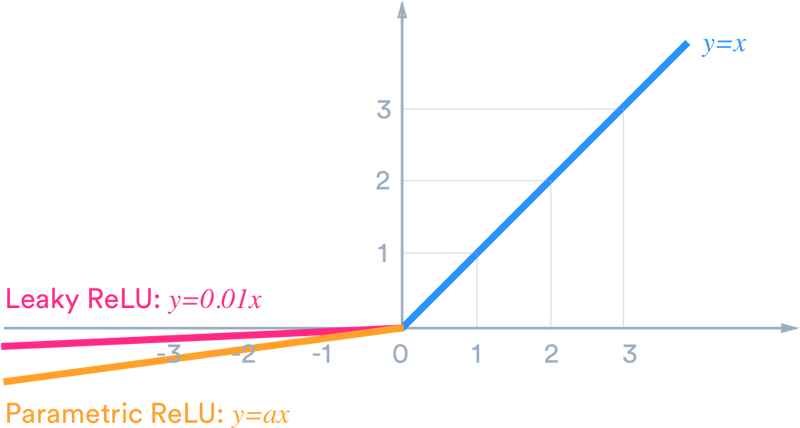
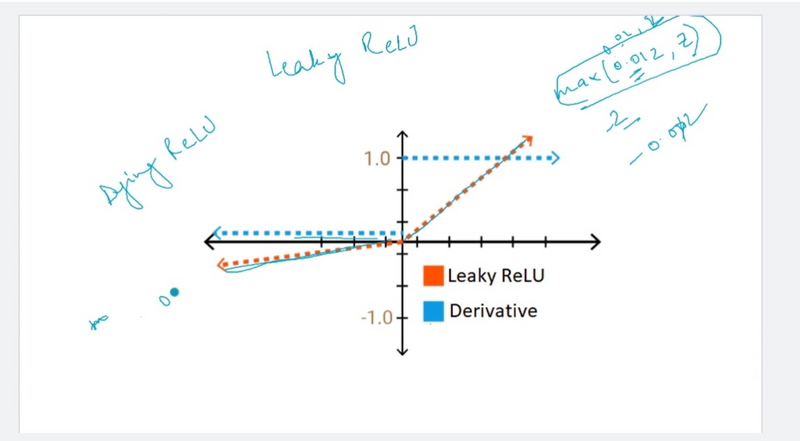
Leaky Rectified Linear Unit (Leaky ReLU):
Leaky ReLU is similar to ReLU but allows a small gradient for negative values (usually a small constant like 0.01).
It helps prevent the "dying ReLU" problem, where neurons become inactive during training.
Example:
def leaky_relu(x, alpha=0.01):
return max(alpha * x, x)
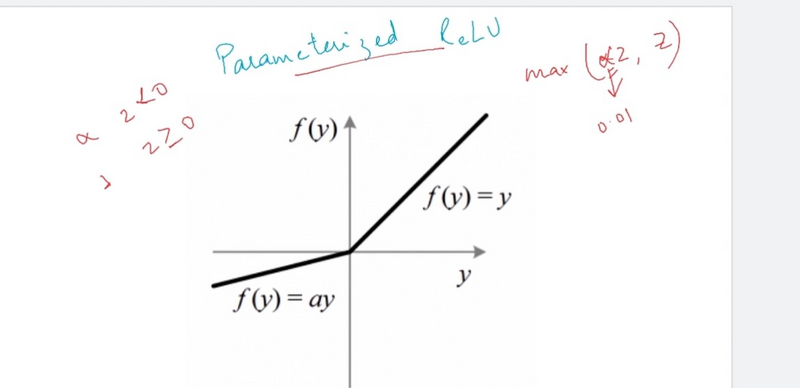
Parametric ReLU (PReLU):
PReLU is an extension of Leaky ReLU where the slope of the negative part is learned during training.
It allows the network to adapt the slope to the data.
Example:
def prelu(x, alpha):
return max(alpha * x, x)
Exponential Linear Unit (ELU):
ELU is similar to ReLU for positive values but has a smooth, differentiable slope for negative values.
It aims to mitigate the vanishing gradient problem.
Example:
def elu(x, alpha=1.0):
return x if x >= 0 else alpha * (np.exp(x) - 1)
Swish:
Swish is a relatively recent activation function that is similar to the sigmoid function but can potentially perform better for certain types of networks.
It has a smooth curve and is easy to optimize.
Example:
def swish(x):
return x / (1 + np.exp(-x))
These are some of the common activation functions used in neural networks. The choice of activation function depends on the problem you're trying to solve, and experimentation is often necessary to determine which works best for your specific dataset and architecture. Each activation function has its strengths and weaknesses, so selecting the right one is an important part of neural network design.
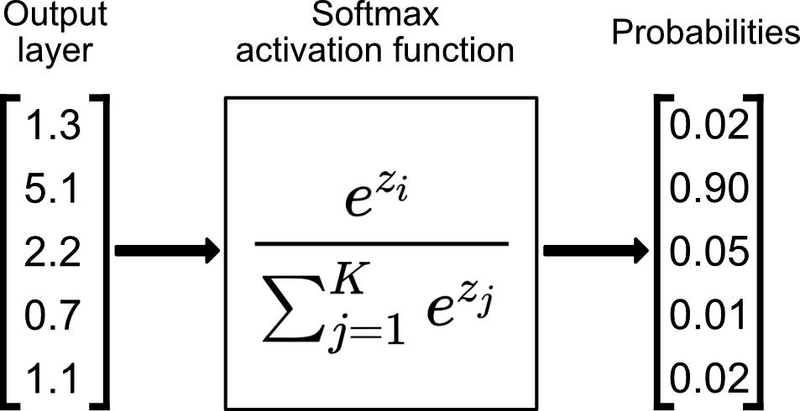
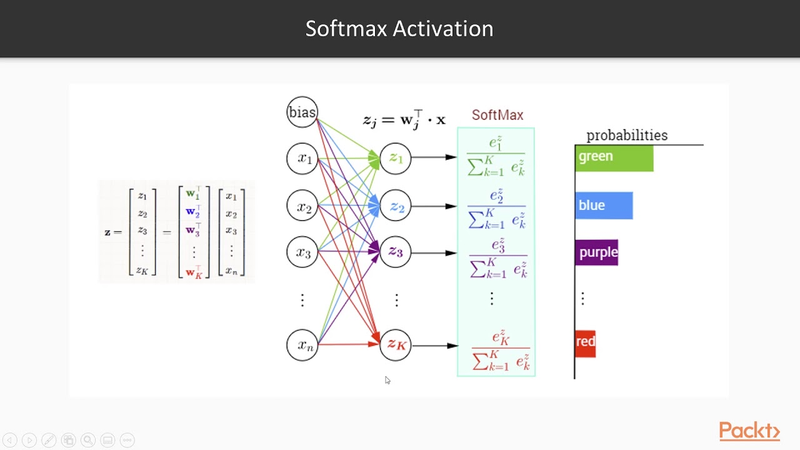
softmax
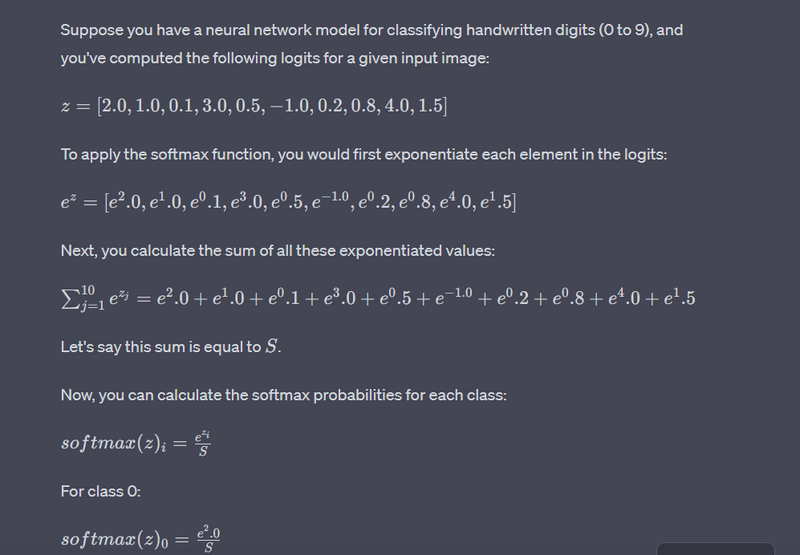
The softmax activation function is a popular activation function used in machine learning, particularly in multi-class classification problems. It's used to transform a vector of real numbers into a probability distribution over multiple classes. The softmax function takes an input vector (often called logits) and normalizes it into a probability distribution. It does this by exponentiating each element in the input vector and then dividing by the sum of all the exponentiated values. The formula for the softmax function for a class i in a vector of logits z is as follows:
where to use which activation function in neural network
note
Most problem used in Relu
for classifiction use sigmoid and softmax
The choice of activation function in a neural network depends on the specific characteristics of your problem, the network architecture, and the challenges you face during training. Here's a guide on where to use which activation function in neural networks with examples:
Sigmoid Activation (Logistic):
Use in the output layer of binary classification problems when you need a probability output between 0 and 1.
Example: Predicting whether an email is spam or not (1 for spam, 0 for not spam).
Hyperbolic Tangent (Tanh):
Suitable for hidden layers when working with data that may have negative values.
Example: Sentiment analysis in natural language processing, where the sentiment score can range from -1 (negative) to 1 (positive).
Rectified Linear Unit (ReLU):
A popular choice for most hidden layers due to its simplicity and effectiveness in overcoming vanishing gradients.
Example: Image classification in deep convolutional neural networks (CNNs) for feature extraction.
Leaky Rectified Linear Unit (Leaky ReLU):
Use when you want to mitigate the "dying ReLU" problem, which can occur when ReLU units become inactive during training.
Example: Training very deep networks, where some neurons may become unresponsive during training.
Parametric ReLU (PReLU):
A variant of Leaky ReLU that allows the slope of the negative part to be learned during training.
Use when you want to adapt the slope to the data.
Example: Image segmentation tasks where different parts of an image may have varying levels of importance.
Exponential Linear Unit (ELU):
Use to mitigate the vanishing gradient problem and achieve faster convergence.
May outperform ReLU when dealing with deep networks and complex tasks.
Example: Natural language processing tasks involving long sequences with dependencies.
Swish:
A more recent activation function that can potentially perform well in various architectures.
Use for experimentation and testing, as it may offer advantages in specific situations.
Example: Neural network architectures where you want to explore alternative activation functions.
In summary, the choice of activation function depends on the specific characteristics of your data and the network architecture. Experimentation is often necessary to determine which activation function works best for your problem. While ReLU is a common choice for hidden layers, you may need to consider other options for addressing issues like vanishing gradients or dying ReLU units. Each activation function has its strengths and weaknesses, and understanding their characteristics is important for effective neural network design.
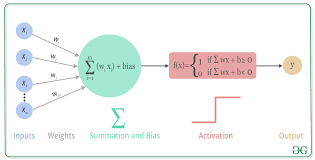
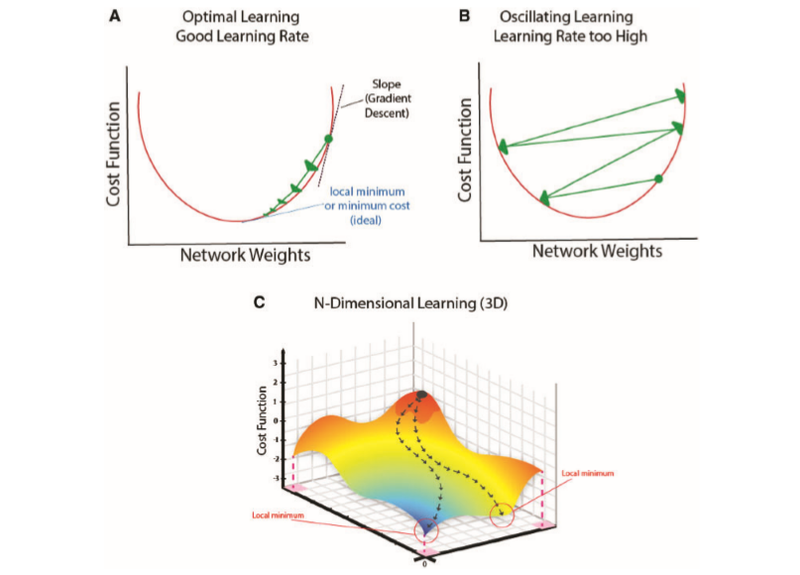
Error in the output is back-propagated through the network and weights are adjusted to minimize the error rate. This is calculated by a cost function. You keep adjusting the weights until they fit all the different training models you put in.
explain the issue or problem in sigmoid and tanh activation function
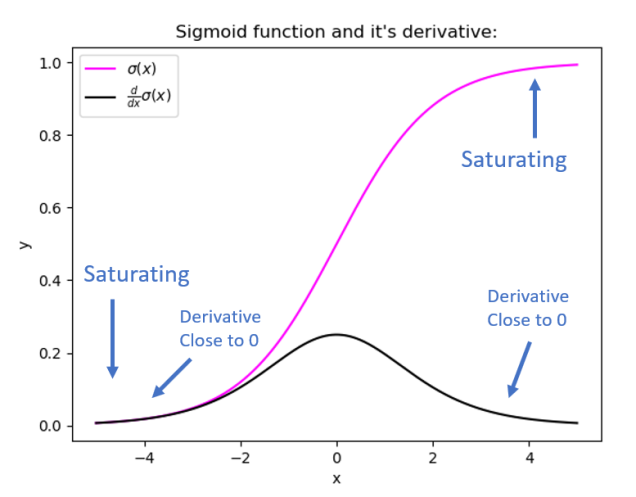
Vanishing Gradient Problem
Hard to compute
Numerical Instability
Exponential Operations
Both the sigmoid and hyperbolic tangent (tanh) activation functions have limitations that can lead to issues in certain neural network architectures. Here are explanations of the problems associated with each activation function along with examples:
Sigmoid Activation Function:
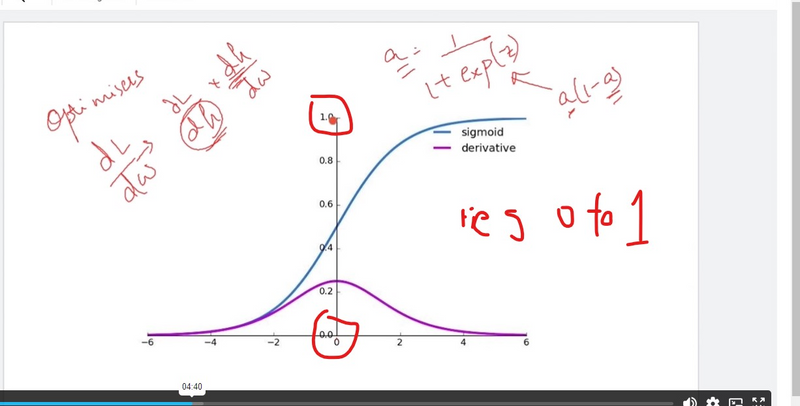
Vanishing Gradient Problem:
The sigmoid function squashes input values to a range between 0 and 1. For extreme inputs (very positive or very negative), the sigmoid function saturates, resulting in extremely small gradients during backpropagation.
This leads to slow convergence and can cause the vanishing gradient problem, especially in deep networks.
Example: Imagine training a deep recurrent neural network (RNN) to generate text, where you encounter a long sequence of words. The gradients during backpropagation become very small as you move backward in time through the sequence, making it challenging to capture long-term dependencies.
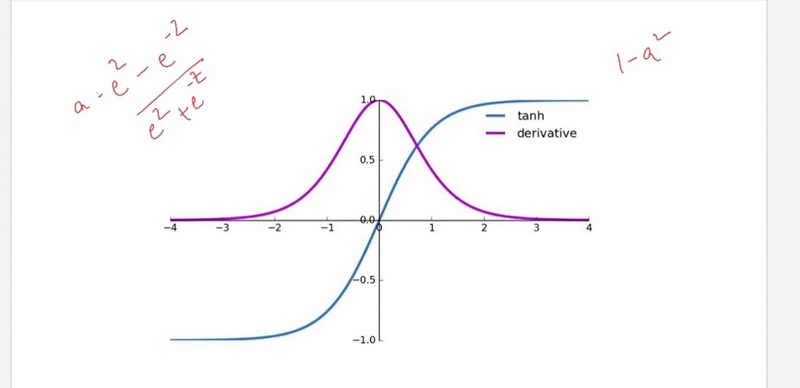
Tanh Activation Function:
Vanishing Gradient Problem:
Like the sigmoid function, the tanh function also saturates for extreme input values, resulting in vanishing gradients.
The tanh function, though zero-centered, still exhibits similar issues with vanishing gradients in deep networks.
Example: In a deep feedforward neural network used for feature extraction from images, as you backpropagate through many layers, the gradients become very small, making it difficult to train deep networks effectively.
Output Range:
The output of the tanh function ranges from -1 to 1, which can be problematic when you have data outside this range. For instance, if the inputs to a tanh-activated layer are large, the outputs may saturate and result in suboptimal learning.
Example: When using tanh as the activation function for hidden layers in a deep reinforcement learning agent, the agent may not effectively learn to handle situations where state variables have values outside the [-1, 1] range, potentially causing suboptimal policies.
In practice, these issues have led to the widespread adoption of the Rectified Linear Unit (ReLU) activation function, which overcomes many of the vanishing gradient problems associated with sigmoid and tanh. ReLU is known for its faster convergence and improved performance in deep neural networks.
It's important to choose the activation function based on the specific problem and network architecture. While sigmoid and tanh may still be suitable for certain scenarios, it's crucial to be aware of their limitations and consider alternatives, such as ReLU, Leaky ReLU, or other advanced activation functions, depending on the nature of your data and the depth of your network.
Exponential Operations:
The sigmoid activation function involves exponentiation, as it calculates the exponential of the input. Exponentiation is computationally more expensive than simple operations like addition and multiplication.
Example: Imagine training a deep neural network for image classification with millions of parameters. The sigmoid activation function is applied at each layer, and the repeated computation of exponentials can slow down the training process, especially during the forward and backward passes.
Numerical Instability:
For extreme input values (very positive or very negative), the sigmoid function can result in numerical instability. Exponentiating large or small numbers can lead to overflow or underflow issues in computer arithmetic.
Example: When dealing with very deep neural networks and gradients that become very small during backpropagation, the sigmoid function's computation may lead to numerical stability issues, causing training to fail or become slow and unstable.
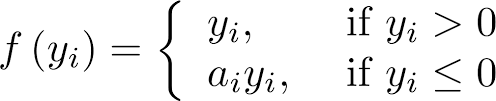
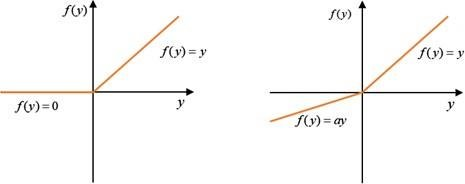







Top comments (0)