Explain the types of error in hypothesis testing

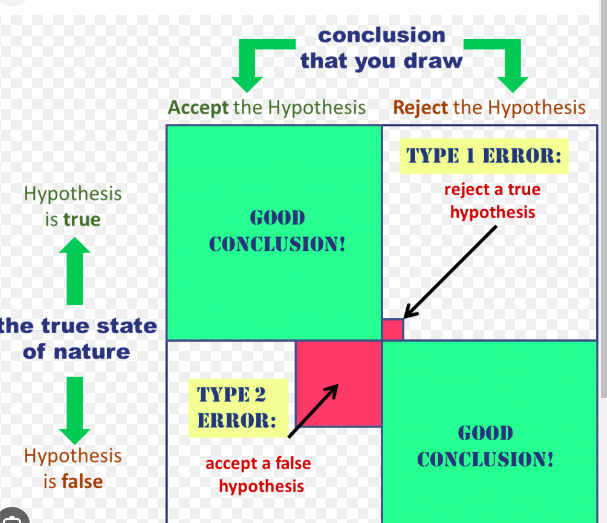
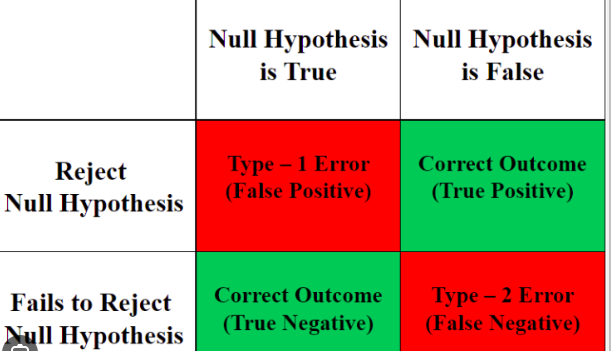
Type I Error (False Positive):
Type I error occurs when we reject the null hypothesis when it is actually true. In other words, it is a false positive result. The significance level (alpha) determines the probability of making a Type I error. If the p-value obtained from the statistical test is lower than the significance level, we reject the null hypothesis, even though it is true.

CONFUSION MATRIX EXAMPLES

many corona +ve and -ve cases come to doctor , now doctor predidicted some positive and some -ve based on symptoms in confusion matrix row side prediction but in lab
give actual result by test blood test and other test
FP==TYPE1 ERROR
FN==TYPE2 ERROR
type2 is more dangerous because u r thinking ur corona negative because of prection/sympotoms/doctor prediction so u roaming/traveling but in lab test u found positive
symptoms==prediction
lab test result/classification model=== actual result
doctor is model
recall== how many positive patient out of total actual positive instance
precision== how many positive parient out of total predicted positive instance
FN== ultimately sign of Tp
F1 SCORE==take some part of recall and take some part of precision mixed of recall and precision
true positive rate is an example of recall
ROC== represents various confusuin matrix for various threshold
if ur threshold value changes then ur confusion matrix,accuracy,recall,precison everything changes
ROC== represent multiple models they predict TPR and FPR

Example:
Consider a pharmaceutical company testing a new drug to treat a certain medical condition. The null hypothesis (H₀) is that the drug has no effect, while the alternative hypothesis (H₁) is that the drug is effective. The Type I error would occur if the company rejects the null hypothesis (H₀) and claims that the drug is effective, even though it has no actual effect.

Consequence: The company may waste resources and time on further development and marketing of an ineffective drug, leading to potential harm or unnecessary costs.

Type II Error (False Negative):
Type II error occurs when we fail to reject the null hypothesis when it is actually false. In other words, it is a false negative result. The probability of making a Type II error is related to the power of the statistical test. A low power indicates a higher likelihood of committing a Type II error.

Example:
Continuing with the pharmaceutical example, a Type II error would occur if the company fails to reject the null hypothesis (H₀) and concludes that the drug is ineffective, even though it actually has a positive effect.

Consequence: In this case, an effective drug might be overlooked, and patients could miss out on a potentially beneficial treatment, resulting in continued suffering or a missed opportunity for improvement.

It is important to note that the occurrence of Type I and Type II errors depends on various factors, including the chosen significance level, sample size, effect size, and statistical power. Balancing these factors and understanding the potential consequences of each type of error is crucial in hypothesis testing.

By considering these types of errors, researchers and decision-makers can make informed choices regarding the interpretation of results and the actions taken based on hypothesis testing.

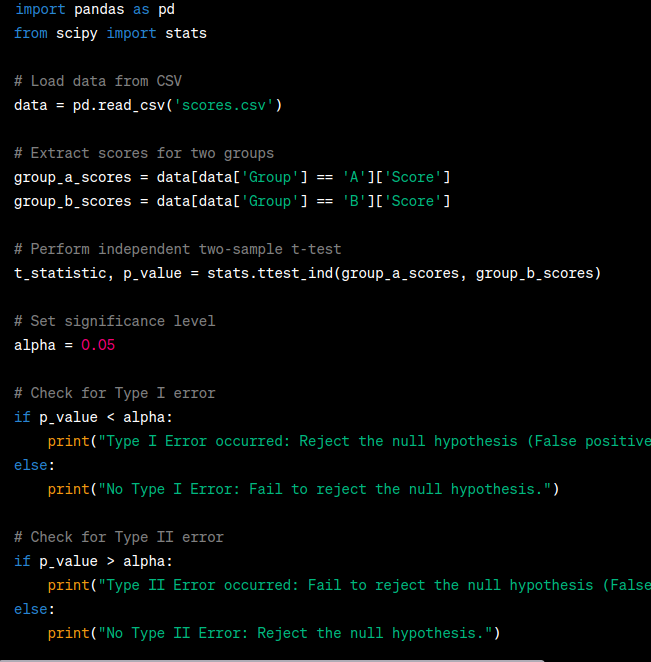
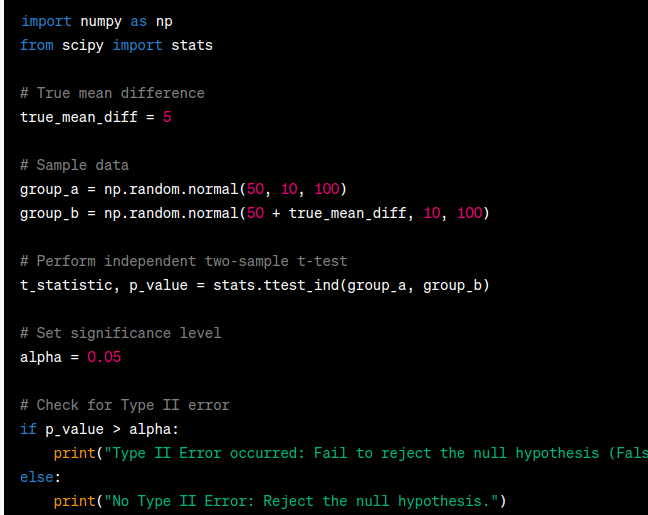
import pandas as pd
from scipy import stats

# Load data from CSV
data = pd.read_csv('scores.csv')

# Extract scores for two groups
group_a_scores = data[data['Group'] == 'A']['Score']
group_b_scores = data[data['Group'] == 'B']['Score']

# Perform independent two-sample t-test
t_statistic, p_value = stats.ttest_ind(group_a_scores, group_b_scores)

# Set significance level
alpha = 0.05

# Check for Type I error
if p_value < alpha:
    print("Type I Error occurred: Reject the null hypothesis (False positive).")
else:
    print("No Type I Error: Fail to reject the null hypothesis.")

# Check for Type II error
if p_value > alpha:
    print("Type II Error occurred: Fail to reject the null hypothesis (False negative).")
else:
    print("No Type II Error: Reject the null hypothesis.")

In this example, we assume that the data is stored in a CSV file named 'scores.csv'. The CSV file should have two columns: 'Group' (representing the group membership, e.g., 'A' and 'B') and 'Score' (representing the exam scores for each group).

The code loads the data from the CSV file using pd.read_csv(). It then extracts the scores for Group A and Group B from the loaded data. The independent two-sample t-test is performed using stats.ttest_ind() to compare the means of the two groups.

Next, we set the significance level (alpha) to 0.05, representing a common threshold for hypothesis testing. We check for Type I error by comparing the obtained p-value with the significance level. If the p-value is less than the significance level, we conclude that a Type I error occurred (rejecting the null hypothesis incorrectly).

Similarly, we check for Type II error by comparing the p-value with the significance level. If the p-value is greater than the significance level, we conclude that a Type II error occurred (failing to reject the null hypothesis when it should have been rejected).

Please note that you need to provide the correct file path and structure the CSV file appropriately with the 'Group' and 'Score' columns for this example to work properly.

QUESTION
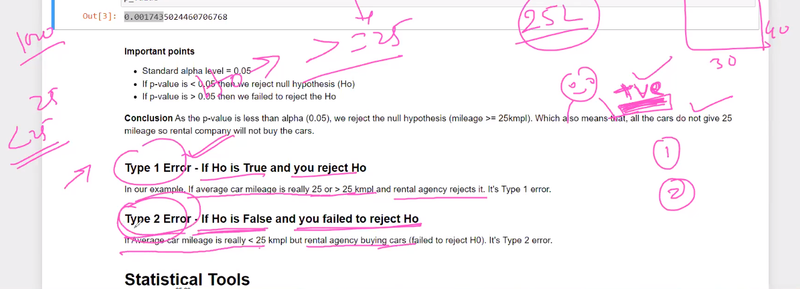
when type I error occur when our hypothesis
when type II error occur when our hypothesis
what is significance level of type I error
what is significance level of type II error
FP and FN is which type of error
define recall and precision
define roc curve represents
which curve give relationship between TPR and FPR on multiple models
What is impact of threshold value changes