Entropy and Gini index are two commonly used impurity metrics in decision trees, which are fundamental components of hyperparameter tuning in machine learning models. Hyperparameter tuning involves selecting the best hyperparameters for a model to improve its performance. Let's explore how entropy and Gini index play important roles in hyperparameter tuning with examples.
Entropy:
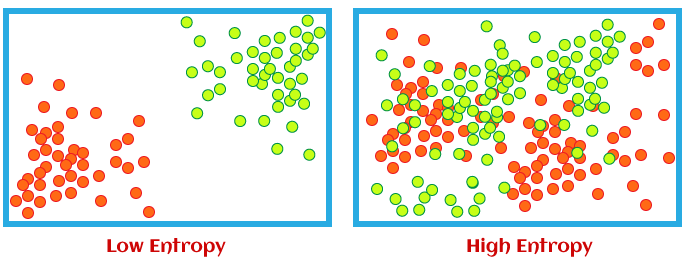
Entropy is a measure of impurity in a set of data. In decision trees, it is used to determine the best split for a node by calculating the information gain. Information gain measures the reduction in entropy after splitting the data based on a particular feature. The goal is to find the feature that results in the highest information gain.
Example:
Suppose you have a binary classification problem to predict whether a person will buy a product or not based on two features: "Age" and "Income." You are building a decision tree model, and you want to determine the best feature to split the data at the root node.
import numpy as np
from sklearn.tree import DecisionTreeClassifier
# Sample data
np.random.seed(42)
X = np.random.randint(20, 60, size=(100, 2))
y = np.random.choice([0, 1], size=(100,))
# Create a decision tree classifier with default hyperparameters
clf = DecisionTreeClassifier()
# Fit the classifier to the data
clf.fit(X, y)
# Get the feature importances (measured by information gain, i.e., entropy)
feature_importances = clf.feature_importances_
print("Feature Importances (Entropy):", feature_importances)
In this example, the feature_importances_ attribute of the trained decision tree classifier will give us the importance of each feature based on the information gain (entropy). Higher values indicate features that are more informative for splitting the data.
Gini Index:
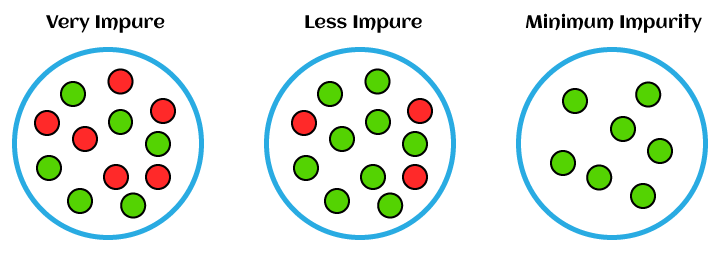
Gini index is another impurity measure used in decision trees. It quantifies the likelihood of misclassifying a randomly chosen element if it were randomly classified according to the distribution of classes in the node. Like entropy, the goal is to find the feature that results in the highest reduction in Gini impurity after splitting the data.
Example:
Continuing from the previous example, we will now use the Gini index as the criterion for splitting the data.
# Create a decision tree classifier with Gini index as the criterion
clf_gini = DecisionTreeClassifier(criterion='gini')
# Fit the classifier to the data
clf_gini.fit(X, y)
# Get the feature importances (measured by Gini index)
feature_importances_gini = clf_gini.feature_importances_
print("Feature Importances (Gini):", feature_importances_gini)
Similar to the previous example, the feature_importances_gini attribute will give us the importance of each feature based on the Gini index.
In hyperparameter tuning, we can use techniques like grid search or random search to explore different combinations of hyperparameters, including criteria (entropy or Gini index) and tree depth, to find the best performing model. By tuning these hyperparameters, we can improve the decision tree model's accuracy and generalization to unseen data
==============================================================
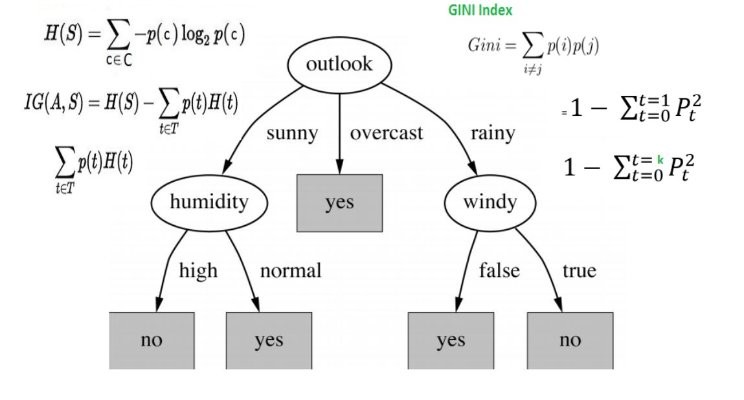
Entropy and Gini index are impurity metrics used to decide the root node and splitting points in a decision tree. Both metrics help determine the best feature and threshold for dividing the data at each node of the tree. The goal is to find the feature and threshold that minimize impurity, resulting in a more informative and effective decision tree.
Let's understand how entropy and Gini index play a role in deciding the root node and splitting points using examples.
Entropy:
Entropy is a measure of impurity in a set of data. In the context of decision trees, it is used to calculate the information gain at each node. Information gain quantifies the reduction in entropy that occurs when the data is split based on a specific feature.
Example:
Suppose we have a binary classification problem to predict whether a student will pass (1) or fail (0) an exam based on two features: "Study Hours" and "Previous Exam Score."
| Study Hours | Previous Exam Score | Result |
|---|---|---|
| 2 | 70 | 0 |
| 4 | 85 | 1 |
| 3 | 75 | 1 |
| 1 | 60 | 0 |
| 5 | 90 | 1 |
We want to create a decision tree to make predictions. To decide the root node, we calculate the entropy for the target variable "Result" (pass or fail) and calculate the information gain for each feature. The feature with the highest information gain will be selected as the root node.
In this example, we'll calculate the entropy for the "Result" variable and information gain for each feature:
import numpy as np
from scipy.stats import entropy
# Sample data
np.random.seed(42)
study_hours = np.random.randint(1, 6, size=100)
previous_exam_score = np.random.randint(60, 91, size=100)
results = np.where((study_hours * 10 + previous_exam_score) >= 300, 1, 0)
# Calculate entropy for the target variable "Result"
target_entropy = entropy(np.bincount(results) / len(results), base=2)
print("Entropy for target variable:", target_entropy)
Once we calculate the entropy for the target variable, we'll calculate the information gain for each feature and select the one with the highest gain as the root node.
Gini Index:
Gini index is another impurity metric used in decision trees. Like entropy, it measures the impurity of a set of data. The Gini index is calculated as the sum of the squared probabilities of each class subtracted from 1.
Example:
Continuing from the previous example, we'll now calculate the Gini index and Gini impurity for each feature:
def gini_impurity(labels):
_, counts = np.unique(labels, return_counts=True)
probabilities = counts / len(labels)
return 1 - np.sum(probabilities ** 2)
# Calculate Gini impurity for the target variable "Result"
target_gini_impurity = gini_impurity(results)
print("Gini impurity for target variable:", target_gini_impurity)
Similar to entropy, once we have the Gini impurity for the target variable, we'll calculate the Gini index and Gini impurity for each feature. The feature with the lowest Gini impurity (highest information gain) will be selected as the root node.
In summary, both entropy and Gini index play essential roles in decision tree algorithms. They help determine the best feature and threshold for splitting the data, ultimately leading to the construction of an effective decision tree for classification tasks.

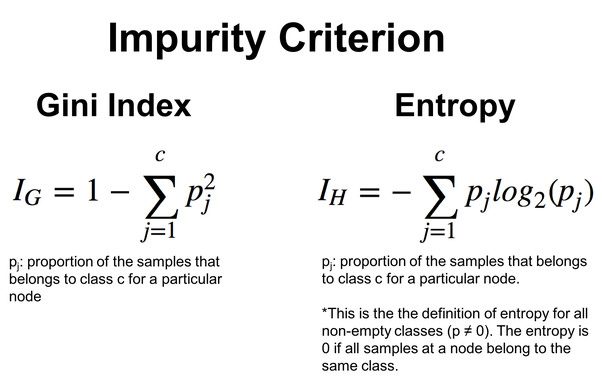

Top comments (0)