How to capture long-term dependencies using LSTM in deep learning

Why Lstm Introduce
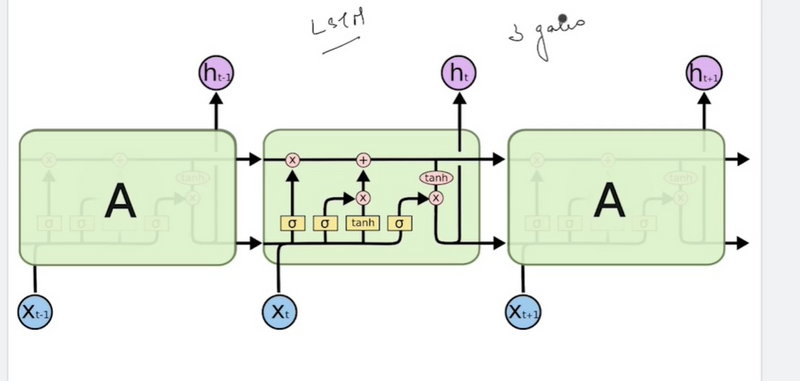
Structure of Lstm
Different type of Gate
Different block or node of LSTM

Why Lstm Introduce

LSTM networks are an extension of recurrent neural networks (RNNs) mainly introduced to handle situations where RNNs fail.

It fails to store information for a longer period of time. At times, a reference to certain information stored quite a long time ago is required to predict the current output. But RNNs are absolutely incapable of handling such “long-term dependencies”.
There is no finer control over which part of the context needs to be carried forward and how much of the past needs to be ‘forgotten’.
Other issues with RNNs are exploding and vanishing gradients (explained later) which occur during the training process of a network through backtracking

Thus, Long Short-Term Memory (LSTM) was brought into the picture. It has been so designed that the vanishing gradient problem is almost completely removed, while the training model is left unaltered. Long-time lags in certain problems are bridged using LSTMs which also handle noise, distributed representations, and continuous values. With LSTMs, there is no need to keep a finite number of states from beforehand as required in the hidden Markov model (HMM). LSTMs provide us with a large range of parameters such as learning rates, and input and output biases.

Structure of Lstm

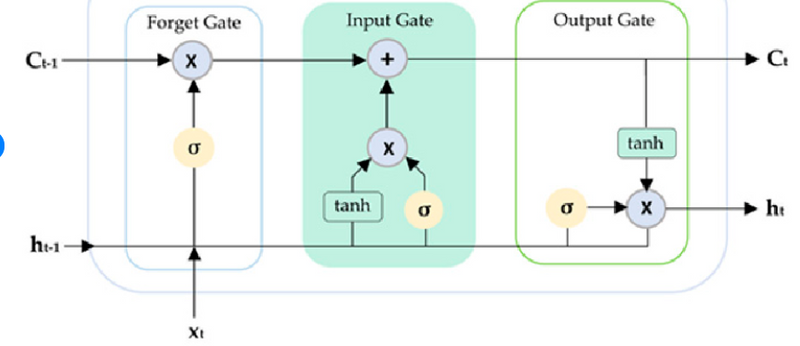
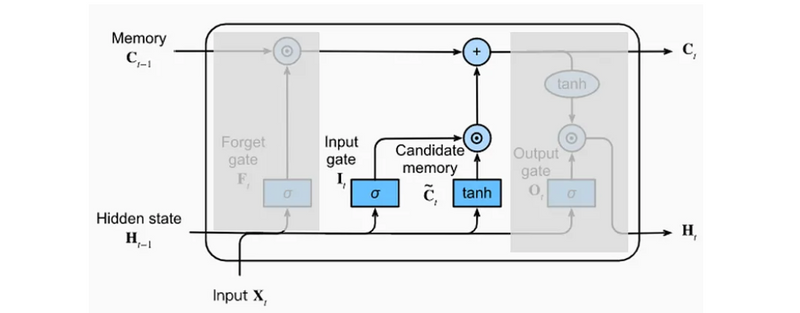
The basic difference between the architectures of RNNs and LSTMs is that the hidden layer of LSTM is a gated unit or gated cell. It consists of four layers that interact with one another in a way to produce the output of that cell along with the cell state. These two things are then passed onto the next hidden layer. Unlike RNNs which have got only a single neural net layer of tanh, LSTMs comprise three logistic sigmoid gates and one tanh layer. Gates have been introduced in order to limit the information that is passed through the cell. They determine which part of the information will be needed by the next cell and which part is to be discarded. The output is usually in the range of 0-1 where ‘0’ means ‘reject all’ and ‘1’ means ‘include all’.

The three gates (forget gate, input gate and output gate) are information selectors. Their task is to create selector vectors. A selector vector is a vector with values between zero and one and near these two extremes.

A selector vector is created to be multiplied, element by element, by another vector of the same size. This means that a position where the selector vector has a value equal to zero completely eliminates (in the multiplication element by element) the information included in the same position in the other vector. A position where the selector vector has a value equal to one leaves unchanged (in the multiplication element by element) the information included in the same position in the other vector.

All three gates are neural networks that use the sigmoid function as the activation function in the output layer. The sigmoid function is used to have, as output, a vector composed of values between zero and one and near these two extremes.

All three gates use the input vector (X) and the hidden state vector coming from the previous instant (H_[t−1]) concatenated together in a single vector. This vector is the input of all three gates.

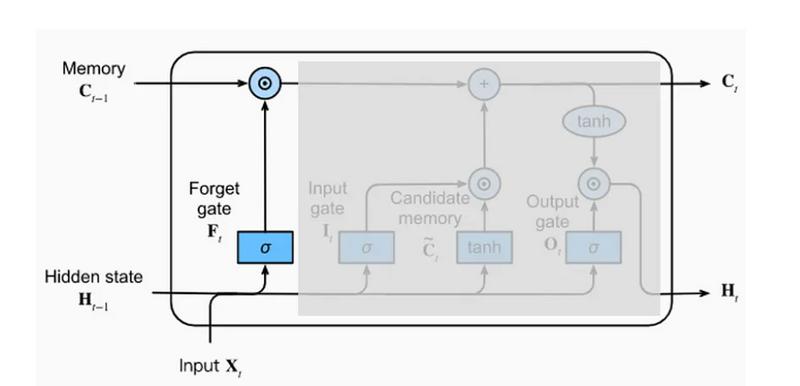
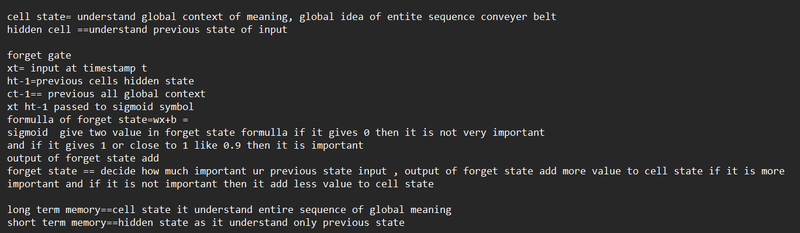
Forget Gate
At any time t, an LSTM receives an input vector (X_[t]) as an input. It also receives the hidden state (H_[t−1]) and cell state (C_[t−1]) vectors determined in the previous instant (t− 1).

The first activity of the LSTM unit is executed by the forget gate. The forget gate decides (based on X_[t] and H_[t−1] vectors) what information to remove from the cell state vector coming from time t− 1. The outcome of this decision is a selector vector.

Figure 2: Forget Gate
The selector vector is multiplied element by element with the vector of the cell state received as input by the LSTM unit. This means that a position where the selector vector has a value equal to zero completely eliminates (in the multiplication) the information included in the same position in the cell state. A position where the selector vector has a value equal to one leaves unchanged (in the multiplication) the information included in the same position in the cell state.

Input Gate and Candidate Memory
After removing some of the information from the cell state received in input (C_[t−1]), we can insert a new one. This activity is carried out by two neural networks: the candidate memory and the input gate. The two neural networks are independent of each other. Their input are the vectors X_[t] and H_[t−1], concatenated together into a single vector.

Figure 3: Input Gate and Candidate Memory
The candidate memory is responsible for the generation of a candidate vector: a vector of information that is candidate to be added to the cell state.

Candidate memory output neurons use hyperbolic tangent function. The properties of this function ensure that all values of the candidate vector are between -1 and 1. This is used to normalize the information that will be added to the cell state.

The input gate is responsible for the generation of a selector vector which will be multiplied element by element with the candidate vector.

The selector vector and the candidate vector are multiplied with each other, element by element. This means that a position where the selector vector has a value equal to zero completely eliminates (in the multiplication) the information included in the same position in the candidate vector. A position where the selector vector has a value equal to one leaves unchanged (in the multiplication) the information included in the same position in the candidate vector.

The result of the multiplication between the candidate vector and the selector vector is added to the cell state vector. This adds new information to the cell state.

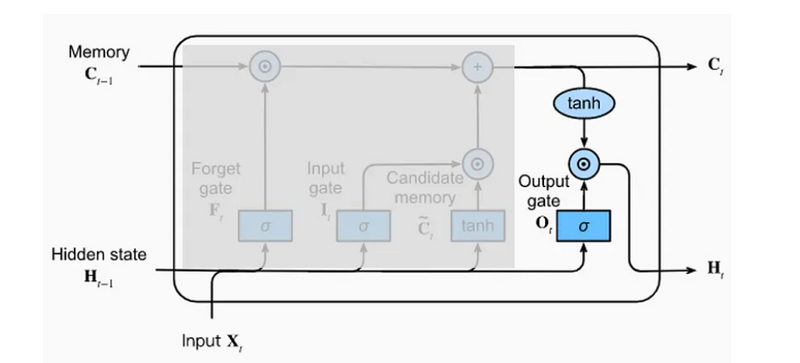
The cell state, after being updated by the operations we have seen, is used by the output gate and passed into the input set used by the LSTM unit in the next instant (t+ 1).

Output Gate
The output gate determines the value of the hidden state outputted by the LSTM (in instant t) and received by the LSTM in the next instant (t+ 1) input set.

Output generation also works with a multiplication between a selector vector and a candidate vector. In this case, however, the candidate vector is not generated by a neural network, but it is obtained simply by using the hyperbolic tangent function on the cell state vector. This step makes the vector values of the cell state normalized within a range of -1 to 1. In this way, after multiplying with the selector vector (whose values are between zero and one), we get a hidden state with values between -1 and 1. This makes it possible to control the stability of the network over time.

Figure 4: Output Gate
The selector vector is generated from the output gate based on the values of X_[t] and H_[t−1] it receives as input. The output gate uses the sigmoid function as the activation function of the output neurons.

Different block or node of LSTM

The architecture of an LSTM can be visualized as a series of repeating “blocks” or “cells”, each of which contains a set of interconnected nodes. Here’s a high-level overview of the architecture:

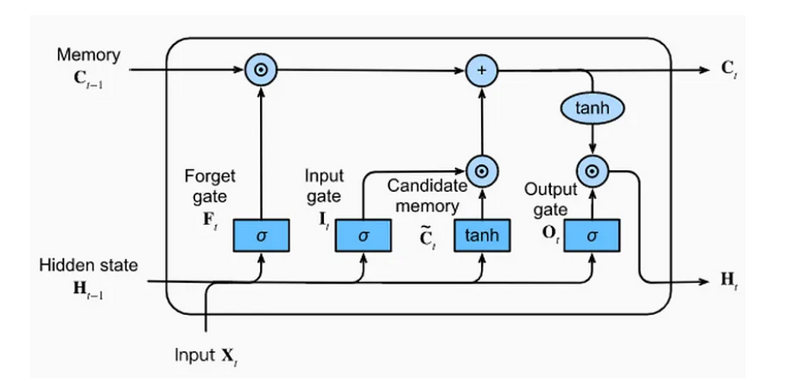
Input: At each time step, the LSTM takes in an input vector, x_t, which represents the current observation or token in the sequence.
Hidden State: The LSTM maintains a hidden state vector, h_t, which represents the current “memory” of the network. The hidden state is initialized to a vector of zeros at the beginning of the sequence.
Cell State: The LSTM also maintains a cell state vector, c_t, which is responsible for storing long-term information over the course of the sequence. The cell state is initialized to a vector of zeros at the beginning of the sequence.
Gates: The LSTM uses three types of gates to control the flow of information through the network: