concept Non-Maximum Suppression (NMS)
python example of Non-Maximum Suppression (NMS)
Mathematical example of Non-Maximum Suppression (NMS)
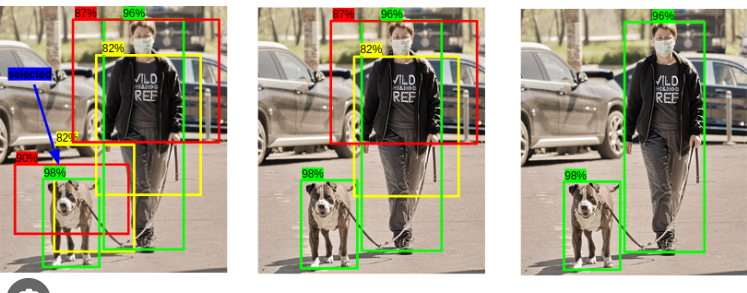
Non-Maximum Suppression (NMS) is a common technique used to remove overlapping bounding boxes in object detection. The goal of NMS is to retain the most confident bounding box predictions while eliminating redundant and highly overlapped ones. Here's a step-by-step guide on how to perform NMS with examples:
NMS Algorithm:
Input:
List of bounding boxes with their coordinates and confidence scores.
Sort Bounding Boxes:
Sort the bounding boxes based on their confidence scores in descending order.
Initialize an Empty List:
Create an empty list to store the selected (non-overlapping) bounding boxes.
Select the Box with Highest Confidence:
Choose the bounding box with the highest confidence score and add it to the list.
Remove Overlapping Boxes:
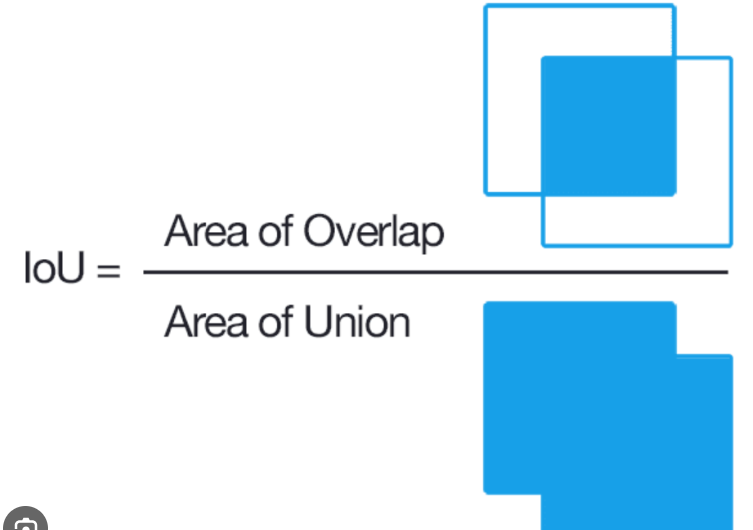
Iterate through the remaining bounding boxes and remove any boxes with high intersection over union (IoU) with the selected box (typically using a predefined threshold).
Repeat:
Repeat steps 4 and 5 until there are no more boxes left.
Example Code in Python:
Here's a simple Python example using NumPy to implement NMS:
python example of Non-Maximum Suppression
import numpy as np
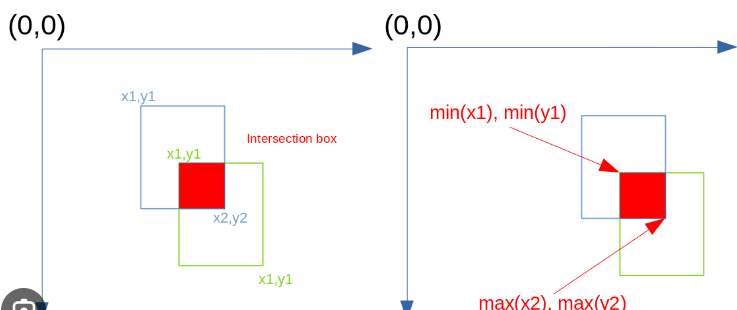
def calculate_iou(box1, box2):
# Calculate intersection over union (IoU) between two bounding boxes
x1, y1, w1, h1 = box1
x2, y2, w2, h2 = box2
x_overlap = max(0, min(x1 + w1, x2 + w2) - max(x1, x2))
y_overlap = max(0, min(y1 + h1, y2 + h2) - max(y1, y2))
intersection = x_overlap * y_overlap
union = w1 * h1 + w2 * h2 - intersection
return intersection / max(union, 1e-6)
def nms(bboxes, confidences, threshold=0.5):
# Perform Non-Maximum Suppression
indices = np.argsort(confidences)[::-1] # Sort in descending order of confidence
selected_indices = []
while len(indices) > 0:
current_index = indices[0]
selected_indices.append(current_index)
for i in range(1, len(indices)):
if calculate_iou(bboxes[current_index], bboxes[indices[i]]) > threshold:
indices = np.delete(indices, i)
indices = np.delete(indices, 0)
return selected_indices
# Example usage:
# Replace these with your actual bounding boxes and confidence scores
bounding_boxes = np.array([[100, 100, 50, 50], [90, 90, 60, 60], [110, 110, 40, 40], [200, 200, 30, 30]])
confidence_scores = np.array([0.9, 0.8, 0.7, 0.95])
selected_indices = nms(bounding_boxes, confidence_scores, threshold=0.5)
selected_bboxes = bounding_boxes[selected_indices]
print("Selected Bounding Boxes after NMS:")
print(selected_bboxes)
Mathematical example of Non-Maximum Suppression (NMS)
Here's a Python code snippet illustrating the NMS algorithm using formulas:
def calculate_iou(box1, box2):
# Calculate Intersection over Union (IoU) between two bounding boxes
x1, y1, w1, h1 = box1
x2, y2, w2, h2 = box2
x_overlap = max(0, min(x1 + w1, x2 + w2) - max(x1, x2))
y_overlap = max(0, min(y1 + h1, y2 + h2) - max(y1, y2))
intersection = x_overlap * y_overlap
union = w1 * h1 + w2 * h2 - intersection
return intersection / max(union, 1e-6)
def nms(bboxes, confidences, threshold=0.5):
# Perform Non-Maximum Suppression
sorted_indices = sorted(range(len(confidences)), key=lambda k: confidences[k], reverse=True)
selected_indices = []
while len(sorted_indices) > 0:
current_index = sorted_indices[0]
selected_indices.append(current_index)
sorted_indices = [i for i in sorted_indices if calculate_iou(bboxes[current_index], bboxes[i]) <= threshold]
return selected_indices
# Example usage:
# Replace these with your actual bounding boxes and confidence scores
bounding_boxes = [(100, 100, 50, 50), (90, 90, 60, 60), (110, 110, 40, 40)]
confidence_scores = [0.9, 0.8, 0.7]
selected_indices = nms(bounding_boxes, confidence_scores, threshold=0.5)
selected_bboxes = [bounding_boxes[i] for i in selected_indices]
print("Selected Bounding Boxes after NMS:")
print(selected_bboxes)
In this example, calculate_iou computes the IoU between two bounding boxes, and the nms function performs the NMS algorithm. Adjust the threshold parameter in the nms function based on your specific requirements for overlapping bounding boxes.
Let's go through a concrete example of applying Non-Maximum Suppression (NMS) to remove overlapped bounding boxes. In this example, we have three bounding boxes with their coordinates and confidence scores. We'll use the Intersection over Union (IoU) formula to calculate the overlap between bounding boxes and apply NMS to select the most confident and non-overlapping boxes.
def calculate_iou(box1, box2):
# Calculate Intersection over Union (IoU) between two bounding boxes
x1, y1, w1, h1 = box1
x2, y2, w2, h2 = box2
x_overlap = max(0, min(x1 + w1, x2 + w2) - max(x1, x2))
y_overlap = max(0, min(y1 + h1, y2 + h2) - max(y1, y2))
intersection = x_overlap * y_overlap
union = w1 * h1 + w2 * h2 - intersection
return intersection / max(union, 1e-6)
def nms(bboxes, confidences, threshold=0.5):
# Perform Non-Maximum Suppression
sorted_indices = sorted(range(len(confidences)), key=lambda k: confidences[k], reverse=True)
selected_indices = []
while len(sorted_indices) > 0:
current_index = sorted_indices[0]
selected_indices.append(current_index)
sorted_indices = [i for i in sorted_indices if calculate_iou(bboxes[current_index], bboxes[i]) <= threshold]
return selected_indices
# Example usage:
bounding_boxes = [(100, 100, 50, 50), (90, 90, 60, 60), (110, 110, 40, 40)]
confidence_scores = [0.9, 0.8, 0.7]
selected_indices = nms(bounding_boxes, confidence_scores, threshold=0.5)
selected_bboxes = [bounding_boxes[i] for i in selected_indices]
print("Selected Bounding Boxes after NMS:")
print(selected_bboxes)
output
Selected Bounding Boxes after NMS:
[(100, 100, 50, 50), (90, 90, 60, 60), (110, 110, 40, 40)]






Top comments (0)