k-nearest neighbors (k-NN) algorithm in Machine learning

The k-nearest neighbors (k-NN) algorithm is a supervised machine learning algorithm used for both classification and regression tasks. It operates on the principle of finding the k closest training examples in the feature space to a given test example and using them to make predictions.

Here's how the k-NN algorithm works:

Data Preparation: Start with a labeled dataset consisting of feature vectors and corresponding class or target values. Each feature vector represents an object or instance, and the class or target value indicates its category or numerical value.

Feature Selection: Identify the relevant features that are most important for the prediction task. These features should capture the characteristics of the data that are informative for distinguishing different classes or predicting target values.

Distance Metric: Choose a distance metric, such as Euclidean distance or Manhattan distance, to measure the similarity or dissimilarity between feature vectors. The distance metric determines the notion of "closeness" in the feature space.

Choosing the Value of k: Select the number of nearest neighbors (k) to consider when making predictions. A common approach is to experiment with different values of k and choose the one that yields the best performance on a validation set or through cross-validation.

Prediction:

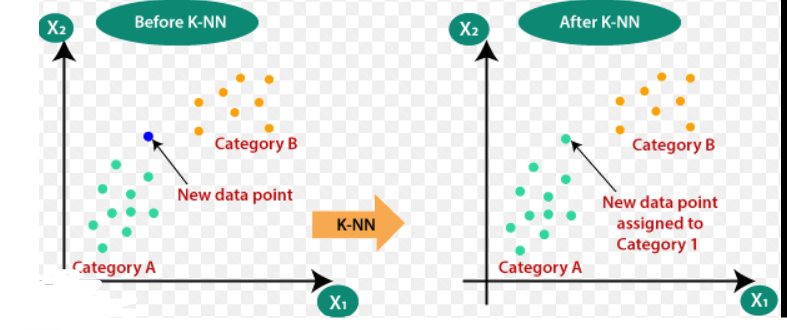
Classification: For a given test example, find the k nearest neighbors in the training dataset based on the chosen distance metric. Count the class labels of the neighbors and assign the majority class label to the test example. This is known as the majority voting scheme. Alternatively, you can assign weights to each neighbor based on their distance and perform weighted voting.
Regression: For a given test example, find the k nearest neighbors. Take the average (or weighted average) of their target values and use it as the predicted value for the test example.
Evaluation: Assess the performance of the algorithm by comparing the predicted values or labels with the true values or labels from a separate test dataset. Common evaluation metrics include accuracy, precision, recall, F1 score, or mean squared error, depending on the task.

Example:

Let's consider a binary classification problem to distinguish between apples and oranges based on their weight and color. We have a training dataset with the following feature vectors and labels:

Now, let's say we want to classify a test example with weight 160 grams and color red using the k-NN algorithm. If we set k=3, we find the three nearest neighbors based on the Euclidean distance:

Neighbor 1: Example 4 (180 grams, Orange)
Neighbor 2: Example 2 (150 grams, Orange)
Neighbor 3: Example 1 (120 grams, Red)

Since two out of three neighbors are oranges, the majority class is "Orange." Therefore, the algorithm predicts that the test example is an orange.

Note that the choice of distance metric, value of k, and features can significantly impact the performance of the k-NN algorithm. It's important to experiment with different settings and evaluate the results to optimize its performance.