One-Tail Test and Two-Tail Test hypothesis in machine learning

In machine learning, hypothesis testing is used to determine the statistical significance of observed data and make decisions based on the results. One-tail and two-tail tests are two common types of hypothesis tests that differ in the directionality of the alternative hypothesis. Here's an explanation of one-tail and two-tail tests with examples:

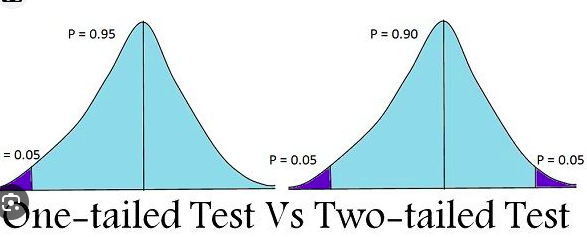
One-Tail Test:
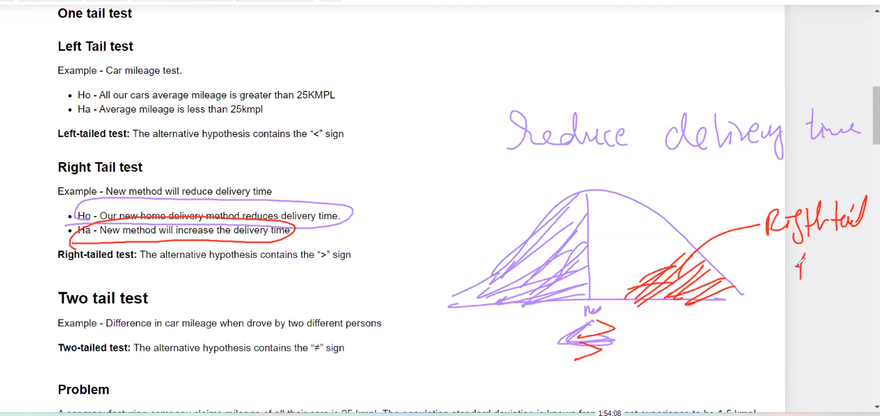
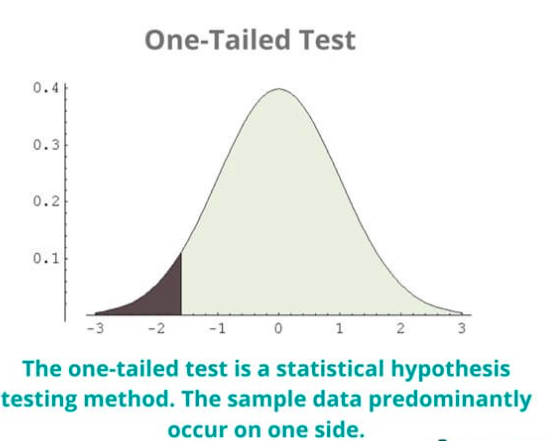
In a one-tail test, the alternative hypothesis is focused on a specific direction or one side of the distribution. It assesses whether the observed data is significantly greater than or less than what is expected under the null hypothesis. The critical region for the test is defined on one side of the distribution.

Example: Consider a scenario where you want to test if a new treatment increases the average response time of a system. The null hypothesis (H₀) would be that the treatment has no effect, and the alternative hypothesis (H₁) would state that the treatment increases the response time. In this case, a one-tail test would be appropriate since the focus is on a specific direction of effect.

Two-Tail Test:
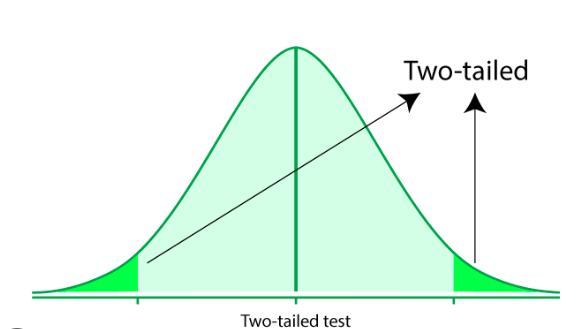
In a two-tail test, the alternative hypothesis considers the possibility of a significant difference in either direction from what is expected under the null hypothesis. It does not specify a specific direction but evaluates if the observed data is significantly different from what is expected. The critical region for the test is divided on both sides of the distribution.

Example: Let's say you want to test if there is a significant difference in the mean weight between two groups of individuals, A and B. The null hypothesis (H₀) would state that there is no difference in the mean weight between the two groups, while the alternative hypothesis (H₁) would state that there is a significant difference, regardless of whether group A is heavier or lighter. In this case, a two-tail test is appropriate since you are interested in any significant difference, regardless of the direction.

The choice between a one-tail or two-tail test depends on the research question and the specific hypothesis being tested. A one-tail test is generally used when there is a prior expectation or specific direction of effect. On the other hand, a two-tail test is more appropriate when the focus is on detecting any significant difference, regardless of the direction.

During hypothesis testing, statistical analysis is performed to calculate a test statistic, such as a t-statistic or z-score, and compare it to a critical value or p-value to make a decision regarding the null hypothesis. The critical value or p-value threshold is determined based on the chosen significance level (e.g., 0.05). If the test statistic falls within the critical region or the p-value is below the threshold, the null hypothesis may be rejected in favor of the alternative hypothesis, indicating a statistically significant result.