Heap Sort in Python
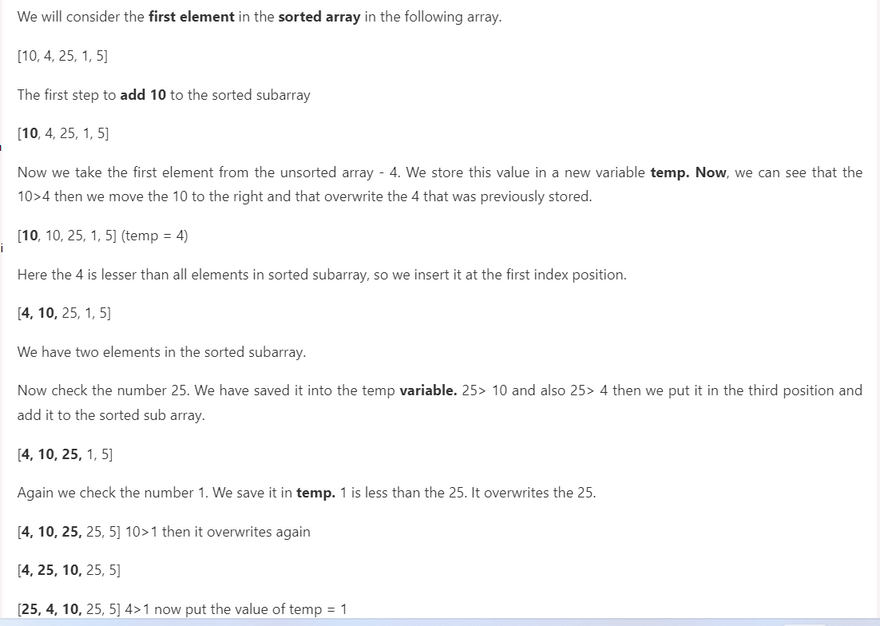
Insertion Sort in Python
Bubble Sort in Python
Merge Sort in Python
Heap Sort in Python
Heap Sort in Python
The heap sort is quite the same as the selection sort, where we find the maximum element and put it at the end. It is based on a comparison sorting algorithm which works on Binary heap data structure. It is the best example of an efficient sorting algorithm.
What is Heap Sort?
Heap sort is an efficient and popular sorting algorithm. The heap sort concept is to "eliminate" the element from the heap part of the list one-by-one and insert them to the sorted part of the list. Before learning more about the heap sorting algorithm, let's discuss the heap data structure.
It is an in-place algorithm, which means a fixed amount of memory is used to store the sorted list, or the memory size doesn't rely on the size of the preliminary list.
For example - We don't need the additional memory stack to store the sorted array and neither recursive call stack. The heapsort algorithm usually implements using the second array to sort the fixed values. This process is quick, simple, natural and easy to implement.
On the other hand, heap sort is unstable, which means it doesn't maintain the comparative order of elements with equal values. It can quickly sort primitive types such as integers and characters, but it has a problem with the complex types and objects.
Let's understand it by the following example -
We have a custom class Student with properties age and name, and several objects of that class in an array, including a student called "Thomas" ages "20" and also "Peter," have aged 20 appear in the same order.
If we sort the array of people by age, then there is no guarantee that "Thomas" would appear before the "Peter" in the sorted array. It can be defined order, but there is no guarantee.
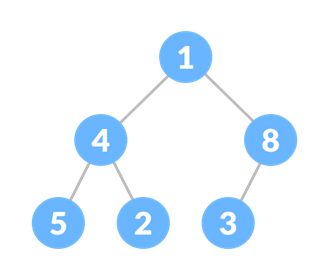
Heap Data Structure
The heap data structure is a complete binary tree that fulfills the heap property. It is also known as the binary heap.
A complete binary tree satisfies the following properties.
- Every level should be filled.
- All the nodes are as far left as possible.
As we can see in the above image of the heap, but it is not sorted. We will not dig in-depth this article because our focus is to explain the Heap sort algorithm, not a heap. In the heap sort, the next smallest element is always the first element.
The heap tree can be the two types - min-heap and max tree. A min-heap is kept a record of the maximum element. A max heap keeps track of the largest element. Heap mainly supports the following operations - delete_minimum(), get_minimum() and add().
The first element of the heap can delete after restoring it. It takes O(log N) time, and that is highly effective.
Implementation
Python provides the in-built functions for sorting elements using heap sort. The functions are given below.
heappush(list, item) -It is used to add the heap element and re-sort it.
heappop(list) - It is used to remove the element and return the element.
heapfy() - It is used to turn the given list into a heap.
Consider the following example for heap sort.
Example -
from heapq import heappop, heappush
def heapsort(list1):
heap = []
for ele in list1:
heappush(heap, ele)
sort = []
# the elements are lift in the heap
while heap:
sort.append(heappop(heap))
return sort
list1 = [27, 21, 55, 15, 60, 4, 11, 17, 2, 87]
print(heapsort(list1))
Output:
[2, 4, 11, 15, 17, 21, 27, 55, 60, 87]
Explanation
In the above code, we have imported the heapq module which consist heappop() and heappush() method. We created the Heapsort Heapsort () method, which takes list1 as an argument. A for loop iterated the list1 and pushed the elements to the empty heap. We used the while loop and sorted element added to the empty sort.
We called the Heapsort Heapsort () function and passed a list. It returned the sorted list.
Sorting Custom Objects
Heap sort is useful for predefined data types, but it is more complicated to handle the user-define data types, such as class objects. We will sort the custom objects in this section.
As we can see, our implementation depends upon the built-in methods. Python provides the following methods.
heapq.nlargest(n, iterable, *key = None) - This method is used to get a list with the n largest element from the dataset, defined by the iterable.
heapq.nsmallest(n, iterable, *key = None) - This method is used to get a list with the n smallest elements from the dataset, which is defined by the iterable.
Let's understand the following implementation of custom objects.
Example -
from heapq import heappop, heappush
class Car:
def __init__(self, model, year):
self.model = model
self.year = year
def __str__(self):
return str.format("Model Name: {}, Year: {}", self.model, self.year)
def __lt__(self, other):
return self.year < other.year
def __gt__(self, other):
return other.__lt__(self)
def __eq__(self, other):
return self.year == other.year
def __ne__(self, other):
return not self.__eq__(other)
def heapsort(list1):
heap = []
for element in list1:
heappush(heap, element)
ordered = []
while heap:
ordered.append(heappop(heap))
return ordered
car1 = Car("Renault", 2001)
car2 = Car("Bentley", 2005)
car3 = Car("Kia", 2014)
car4 = Car("Maruti Suzuki", 1999);
car5 = Car("Nano", 2012)
list1 = [car1, car2, car3, car4, car5]
for c in Heapsort Heapsort (list1):
print(c)
Output:
Model Name: Maruti Suzuki, Year: 1999
Model Name: Renault, Year: 2001
Model Name: Bentley, Year: 2005
Model Name: Nano, Year: 2012
Model Name: Kia, Year: 2014
We have sorted the objects on the year base.
Comparison between Heap sort and Other Algorithm
One of the popular quick sort algorithms is also very efficient, but heap sort is legally used because of its reliability. The heap sort's key benefit is O(nlogn) upper bound as far as the time complexity is fretful.
The heap sort algorithm takes O(nlogn) time in both average and worst-case scenarios while the quick sort is 20% faster in the average case.
The quick sort algorithm becomes slow in predictable situations. There is a chance of the security breach in quick sort since the foul O(n2) can be easily triggered.
Now we compare to the Merge sort, which takes the same time as the heap sort.
Merge sort is much stable and intuitively parallelizable, where heap sort doesn't have such advantages.
Furthermore, Merge sort is faster than the Heap Sort in most cases since they have the same time complexity.
In contrast, Heapsort can be implemented much quickly in-place than Marge sort can.
Insertion Sort in Python
Insertion Sort in Python
The Insertion sort is a straightforward and more efficient algorithm than the previous bubble sort algorithm. The insertion sort algorithm concept is based on the deck of the card where we sort the playing card according to a particular card. It has many advantages, but there are many efficient algorithms available in the data structure.
While the card-playing, we compare the hands of cards with each other. Most of the player likes to sort the card in the ascending order so they can quickly see which combinations they have at their disposal.
The insertion sort implementation is easy and simple because it's generally taught in the beginning programming lesson. It is an in-place and stable algorithm that is more beneficial for nearly-sorted or fewer elements.
The insertion sort algorithm is not so fast because of it uses nested loop for sort the elements.
Let's understand the following terms.
Python Program
# creating a function for insertion
def insertion_sort(list1):
# Outer loop to traverse through 1 to len(list1)
for i in range(1, len(list1)):
value = list1[i]
# Move elements of list1[0..i-1], that are
# greater than value, to one position ahead
# of their current position
j = i - 1
while j >= 0 and value < list1[j]:
list1[j + 1] = list1[j]
j -= 1
list1[j + 1] = value
return list1
# Driver code to test above
list1 = [10, 5, 13, 8, 2]
print("The unsorted list is:", list1)
print("The sorted list1 is:", insertion_sort(list1))
Output:
The unsorted list is: [10, 5, 13, 8, 2]
The sorted list1 is: [2, 5, 8, 10, 13]
Sorting Custom Objects
Python provides the flexibility to change the algorithm using a custom object. We will create a custom class and redefine the actual comparison parameter and try to keep the same code as the above.
We would require to overload the operators in order to sort the objects in a different way. But, we can pass another argument to the insertion_sort() function by using the lambda function. The lambda function is a convenient when calling the sorting method.
Let's understand the following example of sorting custom objects.
First, we are defining the Point class:
Python Program
# Creating Point class
class Point:
def __init__(self, a, b):
self.a = a
self.b = b
def __str__(self):
return str.format("({},{})", self.a, self.b)
def insertion_sort(list1, compare_function):
for i in range(1, len(list1)):
Value = list1[i]
Position = i
while Position > 0 and compare_function(list1[Position - 1], Value):
list1[Position] = list1[Position - 1]
PositionPosition = Position - 1
list1[Position] = Value
U = Point(2,3)
V = Point(4,4)
X = Point(3,1)
Y = Point(8,0)
Z = Point(5,2)
list1 = [U,V,X,Y,Z]
# We sort by the x coordinate, ascending
insertion_sort(list1, lambda x, y: x.a > y.a)
for point in list1:
print(point)
Output:
The points are in the sorted order
(2,3)
(3,1)
(4,4)
(5,2)
(8,0)
Using the above code, we can sort the coordinate points. It will work for any type of the list.
Time Complexity in Insertion Sort
Insertion sort is a slow algorithm; sometimes, it seems too slow for extensive dataset. However, it is efficient for small lists or array.
The time complexity of the insertion sort is - O(n2). It uses the two loops for iteration.
Another important advantage of the insertion sort is that; it is used by the popular sorting algorithm called Shell sort.
The auxiliary space in insertion sort: O(1)
Bubble Sort in Python
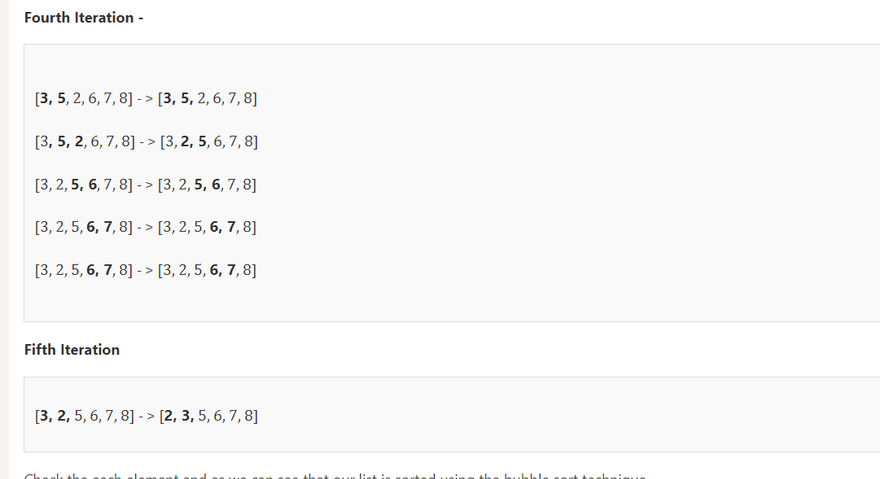
Bubble sort is an easy algorithm among the various sorting algorithms. We learn it as a first sorting algorithm. It is easy to learn and highly intuitive. It can be easy to implement into the code, which is much beneficial for beginner software developers. But it is the worst algorithm for sorting the elements in every except because it checks every time the array is sorted or not.
Let's understand the concepts of the bubble sort.
Concept of Bubble Sort
The bubble sort uses a straightforward logic that works by repeating swapping the adjacent elements if they are not in the right order. It compares one pair at a time and swaps if the first element is greater than the second element; otherwise, move further to the next pair of elements for comparison.
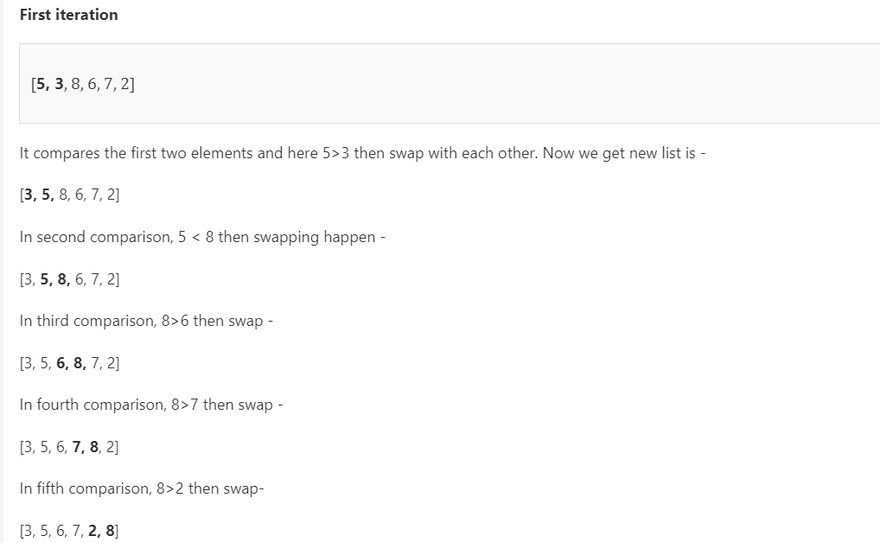
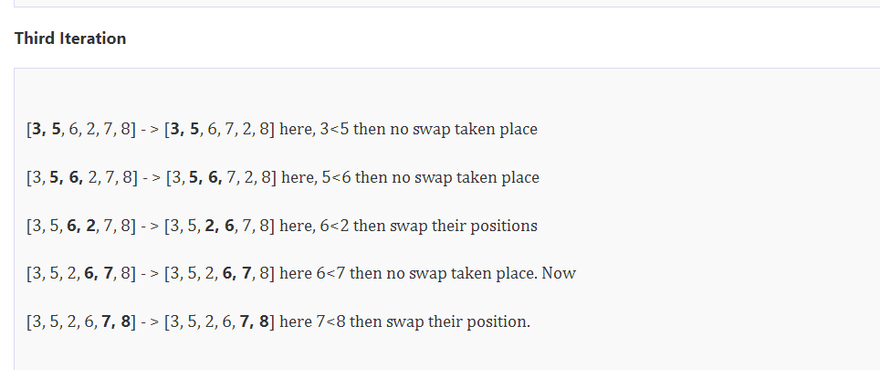
Let's understand it by an example -
Example -
We are creating a list of element, which stores the integer numbers
list1 = [5, 3, 8, 6, 7, 2]
Here the algorithm sort the elements -
Implementation in Python Code
We have already described the technique of bubble sort. Now, we will implement the logic in the Python code.
Program
# Creating a bubble sort function
def bubble_sort(list1):
# Outer loop for traverse the entire list
for i in range(0,len(list1)-1):
for j in range(len(list1)-1):
if(list1[j]>list1[j+1]):
temp = list1[j]
list1[j] = list1[j+1]
list1[j+1] = temp
return list1
list1 = [5, 3, 8, 6, 7, 2]
print("The unsorted list is: ", list1)
# Calling the bubble sort function
print("The sorted list is: ", bubble_sort(list1))
Output:
The unsorted list is: [5, 3, 8, 6, 7, 2]
The sorted list is: [2, 3, 5, 6, 7, 8]
Explanation:
In the above code, we have defined a bubble_sort() function which takes list1 as an argument.
Inside the function, we have defined two for loop - first for loop iterates the complete list and the second for loop iterates the list and the compare the two elements in every outer loop iterations.
The for loop will be terminated when it reaches at the end.
We have defined the condition in the inner for loop; if a first index value is greater than the second index value, swap their positions with each other.
We called the function and passed a list; it iterated and returned the sorted list.
Without using a temp variable
We can also swap the elements without using the temp variable. Python has a very unique syntax. We can use the following lines of code.
Example -
def bubble_sort(list1):
# Outer loop for traverse the entire list
for i in range(0,len(list1)-1):
for j in range(len(list1)-1):
if(list1[j]>list1[j+1]):
# here we are not using temp variable
list1[j],list1[j+1] = list1[j+1], list1[j]
return list1
list1 = [5, 3, 8, 6, 7, 2]
print("The unsorted list is: ", list1)
# Calling the bubble sort function
print("The sorted list is: ", bubble_sort(list1))
Output:
The unsorted list is: [5, 3, 8, 6, 7, 2]
The sorted list is: [2, 3, 5, 6, 7, 8]
Optimization of Python Code Implementation
We can optimize the above code using the two techniques. The swaps are not done; it means list is sorted. In the previous technique - The previous technique will evaluate the complete list though it doesn't seem necessary to do.
We can prevent the unnecessary evaluation using the Boolean flag and checks if any swaps were made in the previous section.
Example -
def bubble_sort(list1):
# We can stop the iteration once the swap has done
has_swapped = True
while(has_swapped):
has_swapped = False
for i in range(len(list1) - 1):
if list1[i] > list1[i+1]:
# Swap
list1[i], list1[i+1] = list1[i+1], list1[i]
has_swapped = True
return list1
list1 = [5, 3, 8, 6, 7, 2]
print("The unsorted list is: ", list1)
# Calling the bubble sort function
print("The sorted list is: ", bubble_sort(list1))
Output:
The unsorted list is: [5, 3, 8, 6, 7, 2]
The sorted list is: [2, 3, 5, 6, 7, 8]
In the second technique, we consider the fact that the iteration is ended when the largest element of the list end up at the end of the list.
The first time, we pass the largest element at the end position using the n position. The second time, we pass through the n-1 position, the second largest element.
In each consecutive iteration, we can compare at one less element than before. More accurately, in the k-th iteration, only need to compare at the first n - k + 1 elements:
Example -
def bubble_sort(list1):
has_swapped = True
total_iteration = 0
while(has_swapped):
has_swapped = False
for i in range(len(list1) - total_iteration - 1):
if list1[i] > list1[i+1]:
# Swap
list1[i], list1[i+1] = list1[i+1], list1[i]
has_swapped = True
total_iteration += 1
print("The number of iteraton: ",total_iteration)
return list1
list1 = [5, 3, 8, 6, 7, 2]
print("The unsorted list is: ", list1)
# Calling the bubble sort funtion
print("The sorted list is: ", bubble_sort(list1))
Output:
The unsorted list is: [5, 3, 8, 6, 7, 2]
The number of iteraton: 6
The sorted list is: [2, 3, 5, 6, 7, 8]
Merge Sort in Python
Merge sort is similar to the quick sort algorithm as works on the concept of divide and conquer. It is one of the most popular and efficient sorting algorithm. It is the best example for divide and conquer category of algorithms.
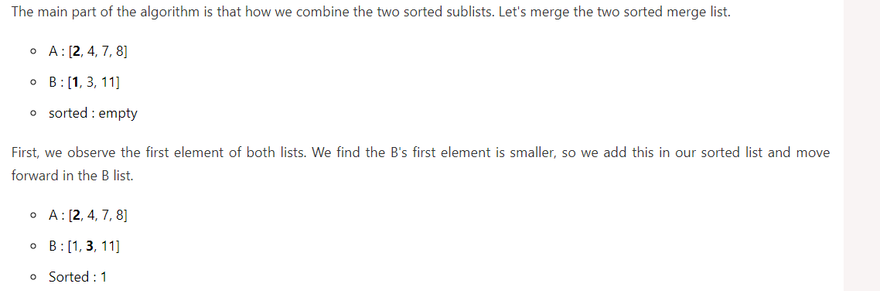
It divides the given list in the two halves, calls itself for the two halves and then merges the two sorted halves. We define the merge() function used to merging two halves.
The sub lists are divided again and again into halves until we get the only one element each. Then we combine the pair of one element lists into two element lists, sorting them in the process. The sorted two element pairs is merged into the four element lists, and so on until we get the sorted list.
Merge Sort Concept
Let's see the following Merge sort diagram.
We have divided the given list in the two halves. The list couldn't be divided in equal parts it doesn't matter at all.
Merge sort can be implement using the two ways - top-down approach and bottom-up approach. We use the top down approach in the above example, which is Merge sort most often used.
The bottom-up approach provides the more optimization which we will define later.






Top comments (0)