The issues of vanishing and exploding gradients are significant challenges when training Recurrent Neural Networks (RNNs). These problems arise due to the way gradients are propagated through the network during training, especially when dealing with long sequences. Let's explore both phenomena, their causes, and potential solutions with examples.
Vanishing Gradient Problem
What is the Vanishing Gradient Problem?
The vanishing gradient problem occurs when the gradients of the loss function become very small as they are backpropagated through the network. As a result, the weights in the earlier layers (or time steps) learn very slowly or not at all, making it difficult for the model to learn long-range dependencies.
Causes
Activation Functions: When using activation functions like the sigmoid or tanh, gradients can shrink significantly during backpropagation. For example, the derivative of the sigmoid function is small for inputs far from zero, leading to small gradients.
Long Sequences: In RNNs, gradients are multiplied by weights at each time step. If these weights are small, the product of many small gradients can result in an extremely small gradient as it propagates back through time.
Example
Imagine an RNN trying to learn a sequence with long dependencies, like in a sentence. If the model needs to connect a word at the beginning of a long sequence to a word at the end, the gradients can diminish exponentially as they are backpropagated through each time step.
Explosion Gradient Problem
What is the Exploding Gradient Problem?
The exploding gradient problem is the opposite of vanishing gradients; it occurs when gradients become excessively large during backpropagation. This can cause the model weights to grow uncontrollably, leading to numerical instability and making it difficult to converge.
Causes
Large Weights: If the weights of the network are initialized too large or grow during training, they can cause the gradients to explode.
Long Sequences: Similar to the vanishing gradient problem, RNNs multiply the gradients by weights at each time step. If these weights are larger than one, the gradients can grow exponentially.
Example
If an RNN is learning a sequence and at each step, the gradients are multiplied by weights larger than one, the gradients will increase rapidly. This can lead to instability, causing the model to diverge during training.
Solutions
Gradient Clipping:
This is a common technique to mitigate the exploding gradient problem. Gradients are clipped to a maximum norm during backpropagation. If the gradients exceed a certain threshold, they are scaled down to keep them within a manageable range.
Implementation Example (in TensorFlow):
from tensorflow.keras import optimizers
optimizer = optimizers.Adam(clipnorm=1.0) # Clip gradients by norm
model.compile(optimizer=optimizer, loss='categorical_crossentropy')
Using LSTM or GRU Cells:
Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) architectures are designed to combat the vanishing gradient problem. They include mechanisms (gates) that help retain information over long sequences, thereby allowing for better learning of long-range dependencies.
Implementation Example (using LSTM):
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense
model = Sequential()
model.add(LSTM(64, input_shape=(timesteps, features), return_sequences=True))
model.add(Dense(10, activation='softmax')) # Output layer
Careful Weight Initialization:
Using proper weight initialization techniques (like Xavier or He initialization) can help maintain gradients in a reasonable range. This minimizes both vanishing and exploding gradients at the beginning of training.
Using Batch Normalization:
Although traditionally used in feedforward networks, applying batch normalization in RNNs can help stabilize training and mitigate the vanishing/exploding gradient issues by normalizing the inputs to each layer.
Gradient Descent
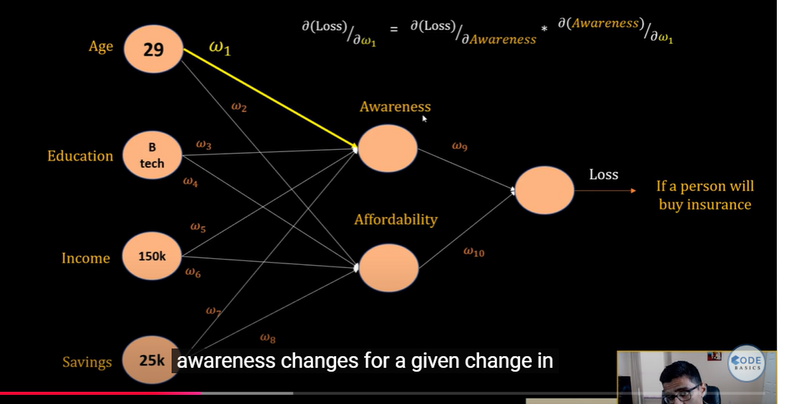
Backpropagation and Chain Rule
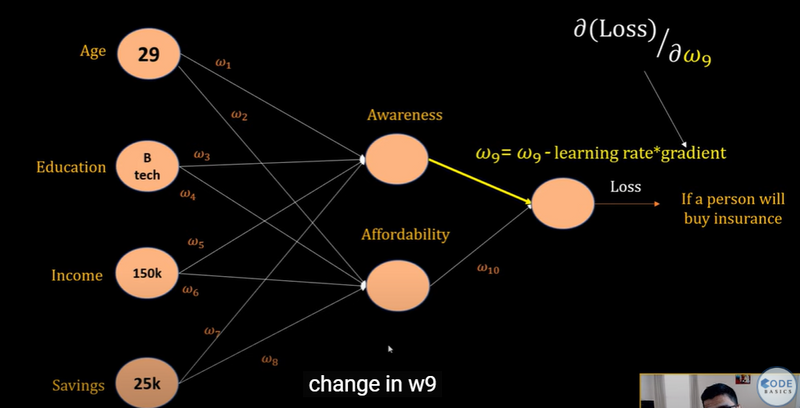
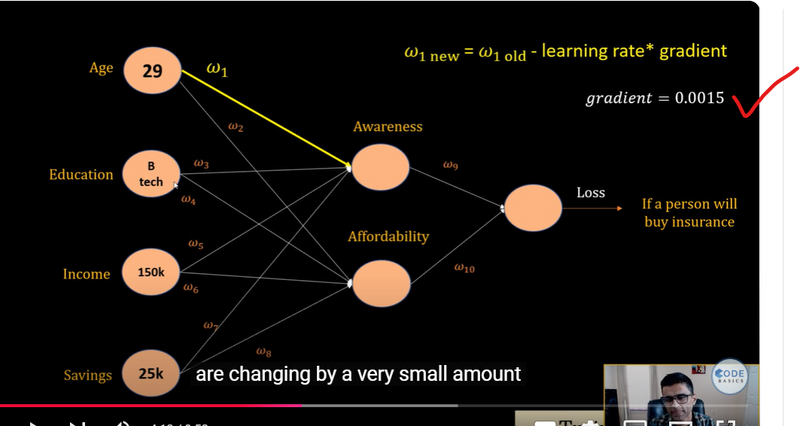
Weight Update Example
Vanishing Gradients
Exploding Gradients
Gradient Calculation Example
Text Example
Solutions to Gradient Problems

















Top comments (0)