Explain Difference between Standardization and normalization

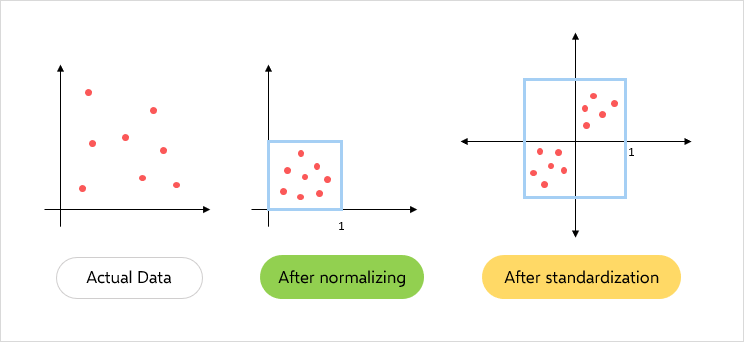
Standardization and normalization are two preprocessing techniques used in machine learning to transform numerical features in your dataset to have specific properties. They are particularly important when working with algorithms that are sensitive to the scale of the input features. Here are the key differences between standardization and normalization:

Standardization (Z-score normalization):

Mean and Variance: Standardization scales the features to have a mean (average) of 0 and a standard deviation of 1. It centers the data around 0 and ensures that it has unit variance.

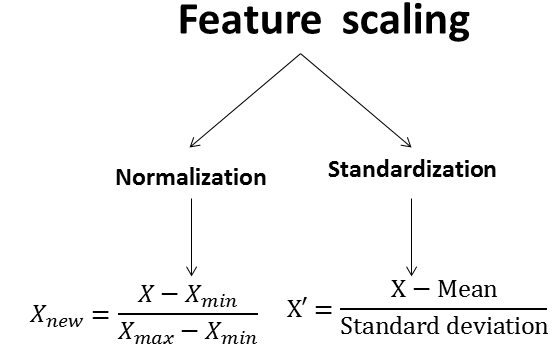
Formula: The standardization formula for a feature 'x' is given by: (x - mean) / standard deviation

Effect on Outliers: Standardization is sensitive to outliers in the data. Outliers can significantly affect the mean and standard deviation, which may impact the transformed values.

Use Cases: Standardization is commonly used when you assume that your data follows a normal distribution, or when you want to remove the scale of the features but preserve their relative distances (e.g., in clustering algorithms like K-means).

Normalization (Min-Max scaling):

Range: Normalization scales the features to a specific range, typically between 0 and 1. It linearly transforms the data so that it falls within this specified range.

Formula: The normalization formula for a feature 'x' is given by: (x - min) / (max - min)

Effect on Outliers: Normalization is less sensitive to outliers because it scales the data based on the minimum and maximum values, and outliers don't disproportionately affect these values.

Use Cases: Normalization is commonly used when the distribution of your data is not necessarily Gaussian (normal) and when you want to ensure that all features have the same scale. It's often used in neural networks and distance-based algorithms like k-nearest neighbors (KNN).

In summary, the key difference between standardization and normalization lies in the scale and centering of the data:

Standardization scales data to have a mean of 0 and a standard deviation of 1. It's appropriate when you assume your data is normally distributed and you want to preserve the shape of the distribution while removing the scale.

Normalization scales data to a specific range (typically 0 to 1) and is suitable when you want to ensure that all features have the same scale regardless of their original distribution. It's less affected by outliers compared to standardization.

The choice between these techniques depends on the characteristics of your data and the requirements of the machine learning algorithm you're using.