Explain the different validation technique of machine learning

Different type of of cross valiadtion technique

Cross-validation is a resampling technique used in machine learning to assess the performance of a model and estimate how well it will generalize to new, unseen data. It involves dividing the dataset into multiple subsets (folds) and using these folds for training and validation in a rotating manner. There are several types of cross-validation techniques, each with its own characteristics and advantages. Here are some common ones:

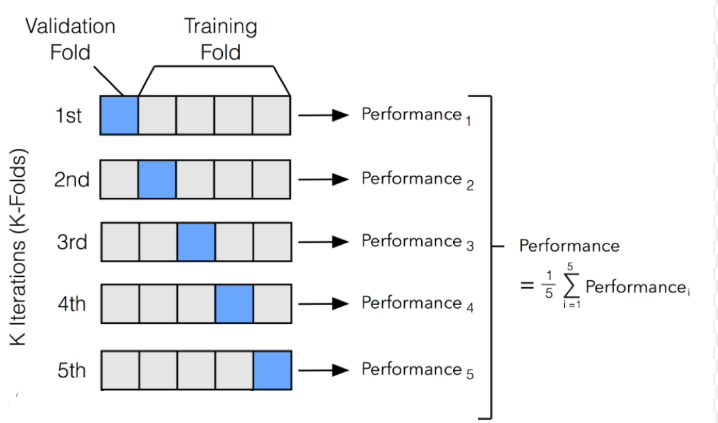
1. K-Fold Cross-Validation:

In k-fold cross-validation, the dataset is divided into*k equal-sized folds. The model is **trained on k-1 folds* and validated on the remaining one. This process is repeated k times, with each fold serving as the validation set exactly once. The final performance metric is the average of the k validation results.
Example:
If you have 1000 data samples and choose k=5, the dataset is divided into 5 folds, each containing 200 samples. The model is trained and validated five times, and the performance metric is the average of the five validation results.

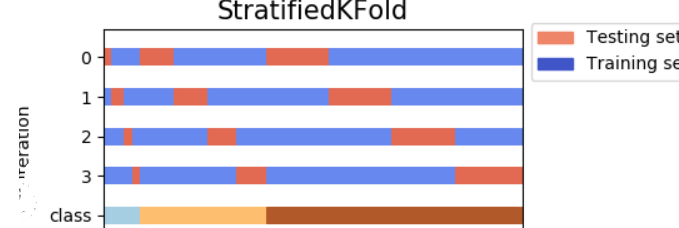
2. Stratified K-Fold Cross-Validation:

Stratified k-fold cross-validation is similar to k-fold cross-validation but ensures that each fold maintains the same class distribution as the original dataset. This is especially useful for imbalanced datasets, where the class distribution may be skewed.
Example:
If you have a binary classification problem with 80% positive samples and 20% negative samples, stratified k-fold cross-validation ensures that each fold also has 80% positive and 20% negative samples.

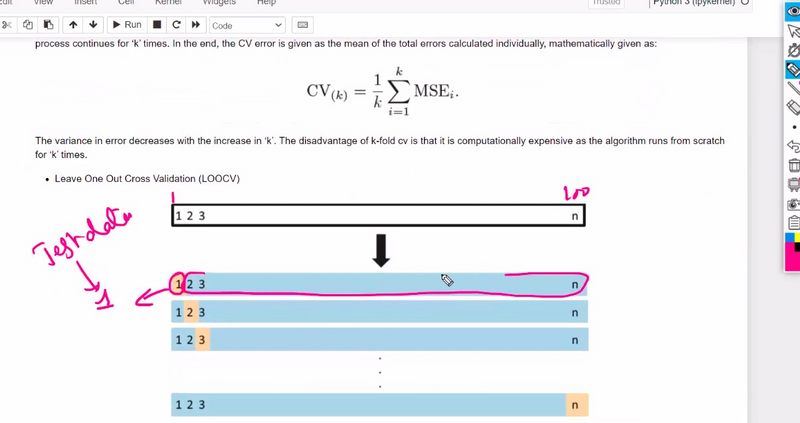
3. Leave-One-Out Cross-Validation (LOOCV):

In LOOCV, each data sample is used as the validation set, and the model is trained on all other samples. This approach is computationally expensive, especially for large datasets, but provides an unbiased estimate of the model's performance.
Example:

If you have **100 data samples**, LOOCV involves **training the model 100 times**, each time leaving out one sample for validation.

4. Leave-P-Out Cross-Validation (LPOCV):

LPOCV is a generalization of LOOCV, where p data samples are left out for validation, and the model is trained on the remaining data. This is less computationally expensive than LOOCV while still providing a relatively unbiased performance estimate.
5. Time Series Cross-Validation:

For time series data, simple random cross-validation might not be appropriate due to the temporal nature of the data. Time series cross-validation involves using a rolling-window approach, where the training data comes before the validation data in time.
Example:
For time series data with monthly observations, you can use the first 80% of data for training and the last 20% for validation. Then, slide the window forward to cover the entire time range.

Cross-validation helps in assessing a model's performance in a robust manner and aids in tuning hyperparameters to find the best configuration. It is crucial to choose the appropriate cross-validation technique based on the nature of your dataset and the problem you are trying to solve.

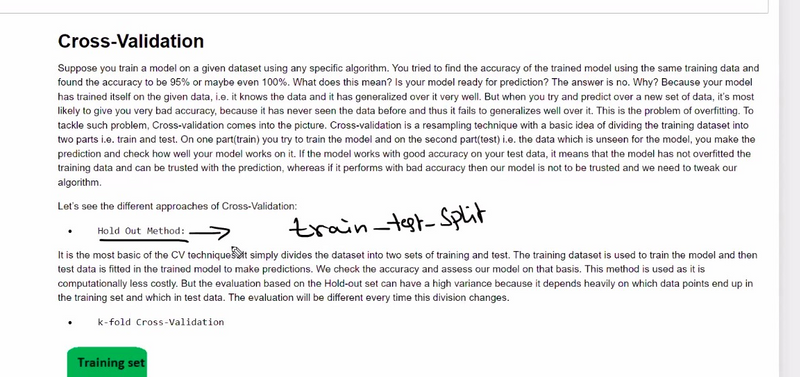
Train-Test Split:
In this technique, the dataset is divided into two parts: a training set and a testing set. The model is trained on the training set and then evaluated on the testing set to assess its performance. The train-test split is typically done with a specified ratio, such as 70% for training and 30% for testing. Example:

from sklearn.model_selection import train_test_split

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train the model on the training set
model.fit(X_train, y_train)

# Evaluate the model on the testing set
accuracy = model.score(X_test, y_test)

Cross-Validation:
Cross-validation is a technique where the dataset is divided into multiple subsets or folds. The model is trained on a combination of these folds while leaving one fold out for testing. This process is repeated for each fold, and the performance is averaged to obtain an overall evaluation of the model. Example:

from sklearn.model_selection import cross_val_score

# Perform cross-validation
scores = cross_val_score(model, X, y, cv=5)

# Get the mean accuracy across all folds
mean_accuracy = scores.mean()

K-Fold Cross-Validation:
K-Fold Cross-Validation is a variant of cross-validation where the dataset is divided into K equal-sized folds. The model is trained on K-1 folds and tested on the remaining fold. This process is repeated K times, with each fold being used as the testing set once. Example:

from sklearn.model_selection import KFold

# Define the number of folds
k = 5

# Perform K-Fold Cross-Validation
kf = KFold(n_splits=k)

# Iterate over the folds
for train_index, test_index in kf.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    model.fit(X_train, y_train)
    accuracy = model.score(X_test, y_test)

Stratified K-Fold Cross-Validation:
Stratified K-Fold Cross-Validation is a variation of K-Fold Cross-Validation that ensures the class distribution in each fold is representative of the overall class distribution. This is particularly useful when dealing with imbalanced datasets. Example:

from sklearn.model_selection import StratifiedKFold

# Define the number of folds
k = 5

# Perform Stratified K-Fold Cross-Validation
skf = StratifiedKFold(n_splits=k)

# Iterate over the folds
for train_index, test_index in skf.split(X, y):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    model.fit(X_train, y_train)
    accuracy = model.score(X_test, y_test)

These are just a few examples of validation techniques in machine learning. The choice of technique depends on the specific problem, dataset characteristics, and available resources.

Leave-One-Out Cross-Validation (LOOCV):
LOOCV is a special case of K-Fold Cross-Validation where K is equal to the number of data points in the dataset. In each iteration, one data point is used as the testing set, and the remaining data is used for training. LOOCV is useful when working with small datasets. Example:

from sklearn.model_selection import LeaveOneOut

loo = LeaveOneOut()

# Iterate over the data points
for train_index, test_index in loo.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    model.fit(X_train, y_train)
    accuracy = model.score(X_test, y_test)

Shuffle Split:
In Shuffle Split, the dataset is randomly shuffled and then split into training and testing sets. This technique allows for multiple iterations with different train-test splits. Example:

from sklearn.model_selection import ShuffleSplit

# Define the number of splits and the test size
n_splits = 5
test_size = 0.2

# Perform Shuffle Split
ss = ShuffleSplit(n_splits=n_splits, test_size=test_size)

# Iterate over the splits
for train_index, test_index in ss.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    model.fit(X_train, y_train)
    accuracy = model.score(X_test, y_test)

Time Series Cross-Validation:
Time Series Cross-Validation is used when dealing with time-series data, where the order of the data points is important. It ensures that the model is evaluated on a realistic time frame. Example:

from sklearn.model_selection import TimeSeriesSplit

# Define the number of splits
n_splits = 5

# Perform Time Series Cross-Validation
tscv = TimeSeriesSplit(n_splits=n_splits)

# Iterate over the splits
for train_index, test_index in tscv.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    model.fit(X_train, y_train)
    accuracy = model.score(X_test, y_test)

Holdout Validation:
Holdout Validation is a simple validation technique where a portion of the dataset is held out as a validation set while the remaining data is used for training. Example:

# Split the data into training, validation, and testing sets
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
X_val, X_test, y_val, y_test = train_test_split(X_val, y_val, test_size=0.5, random_state=42)

# Train the model on the training set
model.fit(X_train, y_train)

# Evaluate the model on the validation set
accuracy = model.score(X_val, y_val)