Defination
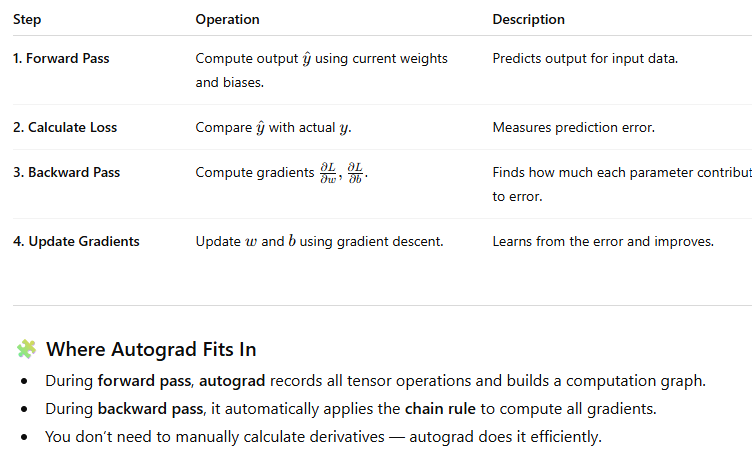
Roles of Autograd
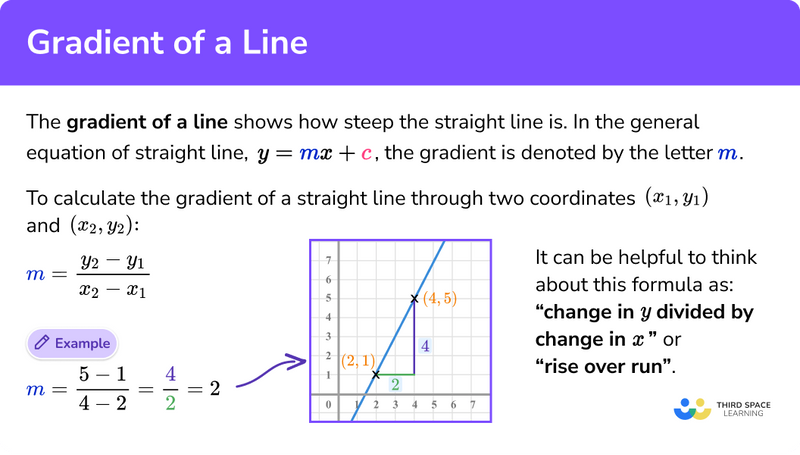
Why Calculate Gradients
Why Differentiation Is Needed
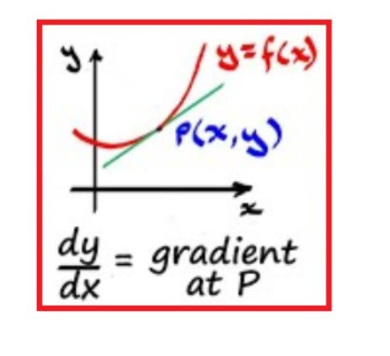
how nested function closely related to deeplearning layers
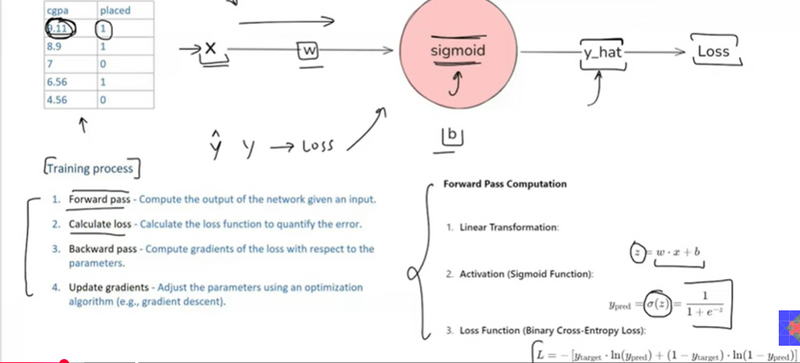
Explain Training process of neural network
When gradient and autograd compute in neural network
Autograd is used in PyTorch to provide automatic differentiation for tensor operations, enabling the system to compute gradients automatically. This is essential for training machine learning models, especially neural networks, using optimization algorithms like gradient descent.
Here are the main roles of PyTorch's autograd:
Automatic Differentiation: It automatically computes gradients (derivatives) for tensor operations, making it easy to optimize parameters in machine learning models without manual calculus.
Recording Computational Graphs: Autograd tracks every operation on tensors requiring gradients in a dynamic directed acyclic graph (DAG). This graph is used to calculate gradients efficiently using the chain rule.
Powering Backpropagation: During training, calling .backward() triggers the backward pass, where autograd computes gradients of the loss function with respect to input parameters—a process essential for updating model weights.
Supports Complex Models: It works seamlessly with simple mathematical expressions, multi-step computations, and deep neural networks, even handling dynamic graph structures or changing computations each iteration.
Integration with Optimizers: Autograd provides gradients needed by optimizers (like SGD, Adam) to perform parameter updates and minimize loss functions in model training.
Custom Autograd Functions: Advanced users can define their own forward and backward computation logic by subclassing autograd.Function, enabling gradient support for custom operations.
Efficient and Scalable: It minimizes code complexity and speeds up large-scale deep learning by efficiently managing memory and computation for gradient tracking and backpropagation.
Calculating gradients and performing differentiation are crucial in machine learning for training models like neural networks using optimization algorithms, primarily gradient descent.
Why Calculate Gradients
Gradients represent the direction and rate of change of the loss function with respect to model parameters (weights and biases).
They tell the optimizer how to adjust parameters (increase or decrease) to reduce the model’s prediction error, measured by the loss function.
By following the negative gradient direction, algorithms like gradient descent iteratively update model parameters to minimize loss and improve prediction accuracy.
Why Differentiation Is Needed
Differentiation forms the mathematical basis for calculating gradients, indicating how a small change in a parameter affects the output and, hence, the loss.
Finding the slope of the loss/cost function allows the model to learn optimal parameter values through many iterations, effectively tuning the network for best performance.
In deep neural networks, differentiation enables backpropagation, which computes gradients for every layer efficiently through the chain rule
how nested function closely related
Nested Functions (Mathematical View)
Nested Functions ↔ Deep Learning Layers
Explain Training process of neural network
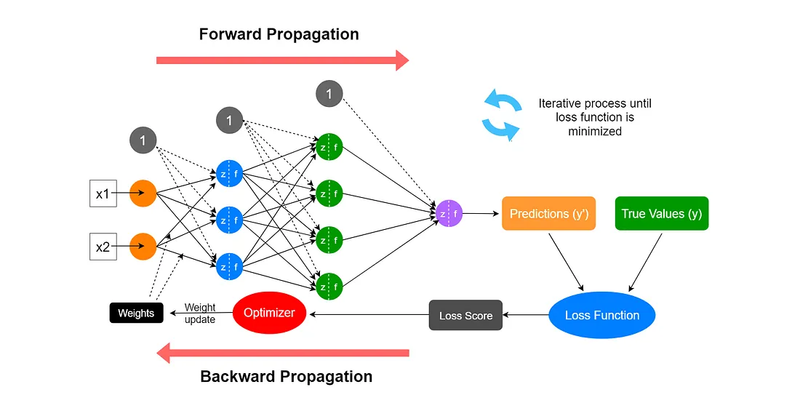
overview-of-a-neural-networks-learning-process
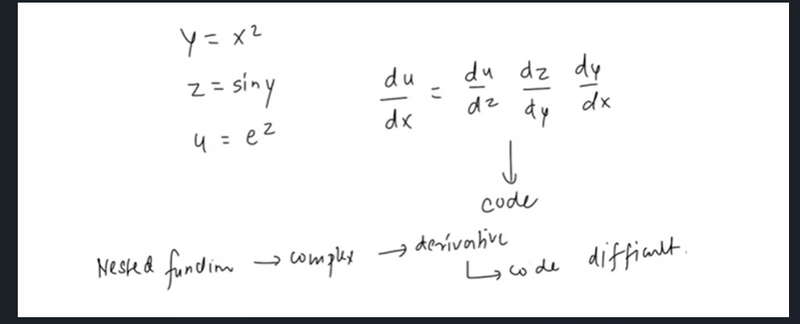
Forward Pass – Compute Output
- Forward Pass — Building the Computational Graph
- During the forward pass:
- You feed data through your network to get predictions.
- Autograd records every operation on tensors that have requires_grad=True.
It builds a computational graph — nodes are tensors, edges are operations.
Calculate Loss – Measure Error
import torch
x = torch.tensor([2.0], requires_grad=True)
w = torch.tensor([3.0], requires_grad=True)
b = torch.tensor([1.0], requires_grad=True)
# Forward pass
z = w * x + b
y_hat = torch.sigmoid(z)
loss = (1 - y_hat)**2
print(loss)
Note:Here autograd does NOT compute gradients yet — it just builds a graph: in forawrd pass we do not compute gradient only calculate loss
in backward pass we compute gradient
x → (w*x + b) → sigmoid → (1 - y_hat)^2 → loss
Backward Pass — Applying the Chain Rule Automatically
loss.backward()
Autograd:
Starts from the scalar loss.
Traverses the graph backward, applying the chain rule step by step.
Accumulates gradients for all leaf tensors (x, w, b).
print(w.grad, b.grad, x.grad)
import torch
# Step 1: Inputs and parameters
x = torch.tensor([2.0], requires_grad=True)
w = torch.tensor([3.0], requires_grad=True)
b = torch.tensor([1.0], requires_grad=True)
# Step 2: Forward pass (autograd tracks operations)
z = w * x + b
y_hat = torch.sigmoid(z)
loss = (1 - y_hat)**2
print("Forward pass output (loss):", loss.item())
# Step 3: Backward pass
loss.backward()
print("Gradient wrt w:", w.grad.item())
print("Gradient wrt b:", b.grad.item())
print("Gradient wrt x:", x.grad.item())
Update Gradients – Adjust Parameters
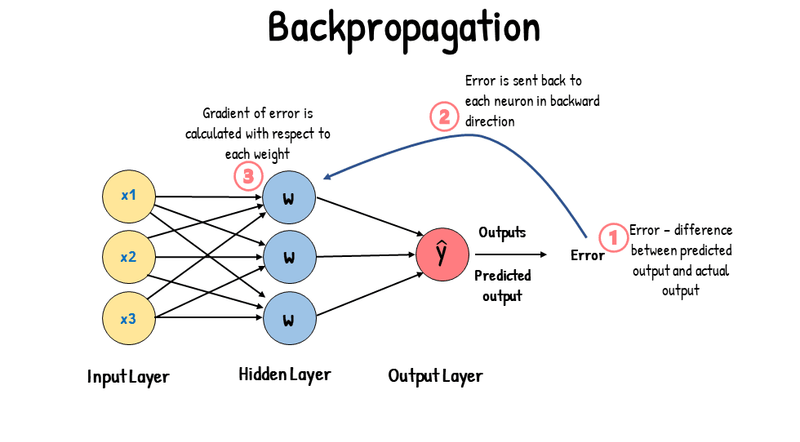
When gradient and autograd compute in neural network
Forward Pass
In this phase:
The model takes inputs → applies transformations → produces output
All mathematical operations are tracked by autograd if requires_grad=True.
import torch
x = torch.tensor([2.0], requires_grad=True)
w = torch.tensor([3.0], requires_grad=True)
b = torch.tensor([1.0], requires_grad=True)
# Forward pass
z = w * x + b
y_hat = torch.sigmoid(z)
loss = (1 - y_hat) ** 2
loss.backward()
loss.backward()
print("dw:", w.grad)
print("db:", b.grad)
print("dx:", x.grad)
Analogy
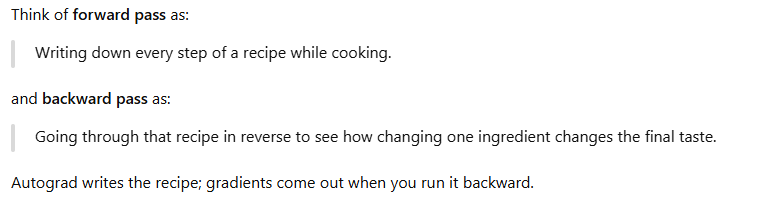
Think of forward pass as:
Writing down every step of a recipe while cooking.
and backward pass as:
Going through that recipe in reverse to see how changing one ingredient changes the final taste.
Autograd writes the recipe; gradients come out when you run it backward.
✅ Final Answer:
Gradients are computed during the backward pass,
but autograd records the necessary graph during the forward pass to make that possible.
SUMMARY
Q*gradient and autograd compute in forward pass or backward pass*
Gradients are computed during the backward pass,
but autograd records the necessary graph during the forward pass to make that possible.

















Top comments (0)